2.2 Linjärt beroende och oberoende
SamverkanLinalgLIU
(Skillnad mellan versioner)
| Rad 9: | Rad 9: | ||
Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/0/01/Kap2_2.pdf 2.2 Linjärt beroende och oberoende]. | Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/0/01/Kap2_2.pdf 2.2 Linjärt beroende och oberoende]. | ||
| + | |||
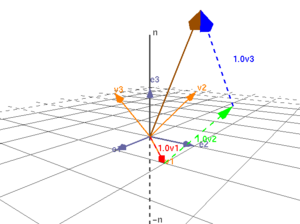
| + | '''''Innan du börjar arbeta med detta moment så kan Du visualisera linjärt beroende genom att klicka på bilden.''''' | ||
<imagemap> | <imagemap> | ||
| Rad 14: | Rad 16: | ||
default [http://webcourses.itn.liu.se/webkurs/LinjartBeroende.jnlp Denna visualisering visar på linjärt beroende] | default [http://webcourses.itn.liu.se/webkurs/LinjartBeroende.jnlp Denna visualisering visar på linjärt beroende] | ||
</imagemap> | </imagemap> | ||
| + | |||
| + | |||
Du har nu läst definitionen på linärt beroende och här kommer några övningar som testar om du har tagit till dig stoffet. | Du har nu läst definitionen på linärt beroende och här kommer några övningar som testar om du har tagit till dig stoffet. | ||
Versionen från 12 september 2011 kl. 12.54
| 2.1 | 2.2 | 2.3 |
Läs textavsnitt 2.2 Linjärt beroende och oberoende.
Innan du börjar arbeta med detta moment så kan Du visualisera linjärt beroende genom att klicka på bilden.
Du har nu läst definitionen på linärt beroende och här kommer några övningar som testar om du har tagit till dig stoffet.
Innehåll |
Övning 3.12
Avgör vilka av följande följder av rumsvektorer som är linjärt oberoende
| a) | \displaystyle \begin{pmatrix}1\\1\\1\end{pmatrix},\ \begin{pmatrix}3\\1\\2\end{pmatrix} | b) | \displaystyle \begin{pmatrix}1\\1\\1\end{pmatrix},\ \begin{pmatrix}3\\1\\2\end{pmatrix},\ \begin{pmatrix}0\\2\\1\end{pmatrix} | c) | \displaystyle \begin{pmatrix}0\\1\\1\end{pmatrix},\ \begin{pmatrix}1\\0\\1\end{pmatrix},\ \begin{pmatrix}1\\1\\0\end{pmatrix} |
Tips och lösning till a)
Tips och lösning till b)
Tips och lösning till c)
Övning 3.13
Ligger vektorerna \displaystyle \boldsymbol{u}=\underline{\boldsymbol{e}}\begin{pmatrix}1\\-2\\1\end{pmatrix}, \displaystyle \boldsymbol{v}=\underline{\boldsymbol{e}}\begin{pmatrix}2\\-1\\-1\end{pmatrix} och \displaystyle \boldsymbol{w}=\underline{\boldsymbol{e}}\begin{pmatrix}-1\\-4\\5\end{pmatrix} i samma plan?
Tips och lösning

 Hämtar...
Hämtar...