14. Minsta kvadratmetoden
SamverkanLinalgLIU
(Ny sida: ==Användarhandledning == Varje kapitel inleds med en länk till en textbok. Tanken är att du läser denna text först. När man läser en matematisk text första gången är det mycket ma...) |
|||
| (10 mellanliggande versioner visas inte.) | |||
| Rad 1: | Rad 1: | ||
| - | + | Läs textavsnitt [http://wiki.math.se/wikis/samverkan/linalg-LIU/img_auth.php/6/60/Kapitel14.pdf 14 Minsta kvadratmetoden]. | |
| - | + | ||
| - | + | Du har nu läst om minsta kvadratmetoden och här kommer några övningar som testar om du har tagit till dig stoffet. | |
| - | ''Tips 1'' Innehåller ofta en hänvisning till texten i textboken. | ||
| - | + | <imagemap> | |
| + | Bild:Minstakvadrat_14_3.png|450px|alt=Alt text | ||
| + | default [http://webcourses.itn.liu.se/webkurs/Inspelningar/Minsta_kvadratmetoden.mov Kicka för att spela upp videon] | ||
| + | </imagemap> | ||
| - | ''Tips 3'' Innehåller ofta mera konkreta råd vad som skall göras. Ibland i form av fragment av lösningen. | ||
| - | '' | + | '''''Klicka på bilden för att se en filminspelning om minstakvadratmetoden.''''' |
| - | Lösningen skall du inte studera förrän du har misslyckats att själv skapa en lösningen med hjälp av Tips 1-3. Det är lätt att lura sig själv genom att läsa igenom lösningen för tidigt och sedan tro att man har förstått. Observera att lösningen inte bara är beräkningar utan innehåller förklarande texter, hänvisning till teorin och en viss struktur. Detta skall även din lösning innehålla. En bra lösning avslutas sedan med ett svar som du, där så är lämpligt, har utvärderat, dvs du har prövat svaret för att säkerställa resultatet. | ||
| - | + | __TOC__ | |
| + | <div class="ovning"> | ||
| + | ===Övning 15.1=== | ||
| + | Ange den linje <math> y=kx+m </math> som i minsta kvadratmening bäst ansluter till punkterna <math> (-1,-3) </math>, <math> (1,-2) </math> och <math> (3,5) </math>. | ||
| + | Rita figur! | ||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 15.1|Tips och lösning|Tips och lösning till U 15.1}} | ||
| + | <div class="ovning"> | ||
| + | ===Övning 15.2=== | ||
| + | a) Ange den linje, <math> y=kx+m </math>, som i minsta kvadratmening ansluter sig bäst till | ||
| - | + | <center><math> | |
| + | \begin{matrix} | ||
| + | \begin{matrix} | ||
| + | x &\vert& \phantom{-}2& \vert& 3& \vert& \phantom{-}4 &\vert& 5\\ | ||
| + | \end{matrix}\\[-3pt] | ||
| + | \rule 150pt 0.4pt 0pt\\ | ||
| + | \begin{matrix} | ||
| + | y &\vert& -2& \vert& 0 & \vert & -1 & \vert & 1 | ||
| + | \end{matrix} | ||
| + | \end{matrix} | ||
| + | </math></center> | ||
| + | b) Beräkna också <math> \sum_{j=1}^4(kx_j+m-y_j)^2 </math>. | ||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 15.2|Tips och lösning till a)|Tips och lösning till U 15.2a | ||
| + | |Tips och lösning till b)|Tips och lösning till U 15.2b}} | ||
| + | |||
| + | |||
| + | |||
| + | <div class="ovning"> | ||
| + | ===Övning 15.3=== | ||
| + | Ange den andragradskurva <math> y=ax^2+bx+c </math>, som i minsta kvadratmening bäst ansluter till följande mätdata | ||
| + | <center><math> | ||
| + | \begin{matrix} | ||
| + | \begin{matrix} | ||
| + | x &\vert& -1& \vert& 0& \vert& 1 &\vert& 2\\ | ||
| + | \end{matrix}\\[-3pt] | ||
| + | \rule 150pt 0.4pt 0pt\\ | ||
| + | \begin{matrix} | ||
| + | y &\vert& \phantom{-}2& \vert& 2 & \vert & 1 & \vert & 0 | ||
| + | \end{matrix} | ||
| + | \end{matrix} | ||
| + | </math></center> | ||
| + | |||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 15.3|Tips och lösning|Tips och lösning till U 15.3}} | ||
| + | |||
| + | |||
| + | |||
| + | <div class="ovning"> | ||
| + | ===Övning 15.4=== | ||
| + | Jämför med Exempel 12.29. | ||
| + | Låt <math> \boldsymbol{u}=(1,0,0)^t </math> och | ||
| + | <center><math> | ||
| + | W=[(1,2,2)^t,(3,0,3)^t]\subset{\bf E}^3. | ||
| + | </math></center> | ||
| + | a) Bestäm med minsta kvadratmetoden (MK-metoden) den ortogonala | ||
| + | projektionen <math> \boldsymbol{u}_{\parallel W} </math>. | ||
| + | |||
| + | b) Bestäm avståndet mellan punkten <math> (1,0,0) </math> och planet <math> W </math>. | ||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 15.4|Tips och lösning till a)|Tips och lösning till U 15.4a | ||
| + | |Tips och lösning till b)|Tips och lösning till U 15.4b}} | ||
| + | |||
| + | |||
| + | |||
| + | <div class="ovning"> | ||
| + | ===Övning 15.5=== | ||
| + | Bestäm med MK-metoden den vektor i | ||
| + | <center><math> | ||
| + | W=[(1,-1,1,-1)^t,(2,0,2,0)^t]\subset{\bf E}^4. | ||
| + | </math></center> | ||
| + | som ligger närmast <math> \boldsymbol{u}=(1,2,3,4)^t </math>. | ||
| + | (Jfr med Exempel 12.30.) | ||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 15.5|Tips och lösning|Tips och lösning till U 15.5}} | ||
| + | |||
| + | |||
| + | |||
| + | <div class="ovning"> | ||
| + | ===Övning 15.6=== | ||
| + | Låt | ||
| + | <center><math> | ||
| + | W=[(1,0,2,2)^t,(1,0,0,1)^t,(1,0,-1,5)^t]\subset{\bf E}^4 | ||
| + | </math></center> | ||
| + | och <math> \boldsymbol{u}=(2,3,6,2)^t </math>. (Jfr med Exempel 12.33.) | ||
| + | |||
| + | a) Bestäm med MK-metoden den ortogonala projektionen | ||
| + | <math> \boldsymbol{u}_{\parallel W} </math>. | ||
| + | |||
| + | b) Bestäm avståndet mellan punkten <math> (2,3,6,2) </math> och hyperplanet <math> W </math>. | ||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 15.6|Tips och lösning till a)|Tips och lösning till U 15.6a | ||
| + | |Tips och lösning till b)|Tips och lösning till U 15.6b}} | ||
| + | |||
| + | |||
| + | <div class="ovning"> | ||
| + | ===Övning 15.7=== | ||
| + | Jämför med Exempel 12.34. Betrakta underrummet | ||
| + | <center><math> | ||
| + | W=\{\boldsymbol{x}\in{\bf E}^3:\ 2x_1-x_2-2x_3=0\}. | ||
| + | </math></center> | ||
| + | Låt <math> \boldsymbol{u}=(x_1,x_2,x_3)^t\in{\bf E}^3 </math> vara godtycklig. | ||
| + | |||
| + | a) Bestäm m.h.a. MK-metoden den ortogonala projektionen <math> P_{W^\perp}(\boldsymbol{u}) </math>. | ||
| + | |||
| + | b) Enligt Exempel 12.34 så är <math> W=[(2,2,1)^t,(1,-2,2)]^t </math>. | ||
| + | Bestäm m.h.a. MK-metoden den ortogonala projektionen | ||
| + | <math> P_{W}(\boldsymbol{u}) </math>. | ||
| + | </div>{{#NAVCONTENT:Svar|Svar till U 15.7|Tips och lösning till a)|Tips och lösning till U 15.7a | ||
| + | |Tips och lösning till b)|Tips och lösning till U 15.7b}} | ||
Nuvarande version
Läs textavsnitt 14 Minsta kvadratmetoden.
Du har nu läst om minsta kvadratmetoden och här kommer några övningar som testar om du har tagit till dig stoffet.
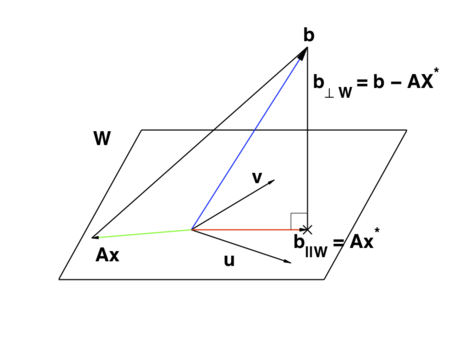
Klicka på bilden för att se en filminspelning om minstakvadratmetoden.
Innehåll |
Övning 15.1
Ange den linje \displaystyle y=kx+m som i minsta kvadratmening bäst ansluter till punkterna \displaystyle (-1,-3) , \displaystyle (1,-2) och \displaystyle (3,5) . Rita figur!
Övning 15.2
a) Ange den linje, \displaystyle y=kx+m , som i minsta kvadratmening ansluter sig bäst till
\begin{matrix} \begin{matrix}
x &\vert& \phantom{-}2& \vert& 3& \vert& \phantom{-}4 &\vert& 5\\
\end{matrix}\\[-3pt] \rule 150pt 0.4pt 0pt\\ \begin{matrix}
y &\vert& -2& \vert& 0 & \vert & -1 & \vert & 1
\end{matrix} \end{matrix}
b) Beräkna också \displaystyle \sum_{j=1}^4(kx_j+m-y_j)^2 .
Övning 15.3
Ange den andragradskurva \displaystyle y=ax^2+bx+c , som i minsta kvadratmening bäst ansluter till följande mätdata
\begin{matrix} \begin{matrix}
x &\vert& -1& \vert& 0& \vert& 1 &\vert& 2\\
\end{matrix}\\[-3pt] \rule 150pt 0.4pt 0pt\\ \begin{matrix}
y &\vert& \phantom{-}2& \vert& 2 & \vert & 1 & \vert & 0
\end{matrix} \end{matrix}
Övning 15.4
Jämför med Exempel 12.29. Låt \displaystyle \boldsymbol{u}=(1,0,0)^t och
W=[(1,2,2)^t,(3,0,3)^t]\subset{\bf E}^3.
a) Bestäm med minsta kvadratmetoden (MK-metoden) den ortogonala projektionen \displaystyle \boldsymbol{u}_{\parallel W} .
b) Bestäm avståndet mellan punkten \displaystyle (1,0,0) och planet \displaystyle W .
Övning 15.5
Bestäm med MK-metoden den vektor i
W=[(1,-1,1,-1)^t,(2,0,2,0)^t]\subset{\bf E}^4.
som ligger närmast \displaystyle \boldsymbol{u}=(1,2,3,4)^t . (Jfr med Exempel 12.30.)
Övning 15.6
Låt
W=[(1,0,2,2)^t,(1,0,0,1)^t,(1,0,-1,5)^t]\subset{\bf E}^4
och \displaystyle \boldsymbol{u}=(2,3,6,2)^t . (Jfr med Exempel 12.33.)
a) Bestäm med MK-metoden den ortogonala projektionen \displaystyle \boldsymbol{u}_{\parallel W} .
b) Bestäm avståndet mellan punkten \displaystyle (2,3,6,2) och hyperplanet \displaystyle W .
Övning 15.7
Jämför med Exempel 12.34. Betrakta underrummet
W=\{\boldsymbol{x}\in{\bf E}^3:\ 2x_1-x_2-2x_3=0\}.
Låt \displaystyle \boldsymbol{u}=(x_1,x_2,x_3)^t\in{\bf E}^3 vara godtycklig.
a) Bestäm m.h.a. MK-metoden den ortogonala projektionen \displaystyle P_{W^\perp}(\boldsymbol{u}) .
b) Enligt Exempel 12.34 så är \displaystyle W=[(2,2,1)^t,(1,-2,2)]^t . Bestäm m.h.a. MK-metoden den ortogonala projektionen \displaystyle P_{W}(\boldsymbol{u}) .

 Hämtar...
Hämtar...