SamverkanLinalgLIU

Versionen från 12 september 2011 kl. 14.08 (redigera) Geoba (Diskussion | bidrag) ← Gå till föregående ändring		Versionen från 12 september 2011 kl. 14.17 (redigera) (ogör) Geoba (Diskussion | bidrag) Gå till nästa ändring →
Rad 107:		Rad 107:
	Tips och lösning|Tips och lösning till övning 17.16}}		Tips och lösning|Tips och lösning till övning 17.16}}
-	[http://webstaff.itn.liu.se/~geoba/TNA002/webkurs/MatrixProj.jnlp Bestämma matris för en ortogonal projektion]	+
		+	'''''Innan Du börjar arbeta med detta moment så kan Du bestämma matrisen för en ortogonal projektion genom att klicka på bilden.'''''
		+
		+	<imagemap>
		+	Bild:MatrixProj.png|350px|alt=Alt text
		+	default [http://webcourses.itn.liu.se/webkurs/MatrixProj.jnlp Du kan bestämma matrisen för en ortogonal]
		+	</imagemap>
		+
		+
		+	'''''Innan Du börjar arbeta med detta moment så kan Du bestämma matrisen för en spegling genom att klicka på bilden.'''''
		+
		+	<imagemap>
		+	Bild:MatrixSpeg.png|350px|alt=Alt text
		+	default [http://webcourses.itn.liu.se/webkurs/MatrixSpeg.jnlp Du kan bestämma matrisen för en spegling]
		+	</imagemap>
		+

---

Versionen från 12 september 2011 kl. 14.17

16.1

16.2

16.3

16.4

16.5

16.6

16.7

16.8

16.9

16.10

16.11

Läs textavsnitt 16.3 Projektion och Spegling

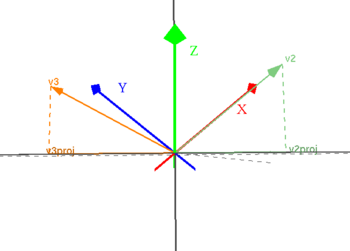
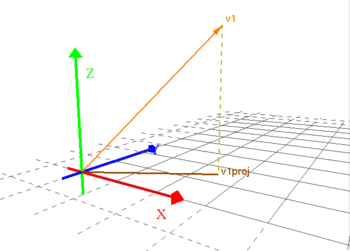
Innan Du börjar arbeta med detta moment så kan Du visualisera ortogonal projektion på ett plan genom att klicka på bilden.

Innan Du börjar arbeta med detta moment så kan Du visualisera ortogonal projektion på ett plan genom att klicka på bilden.

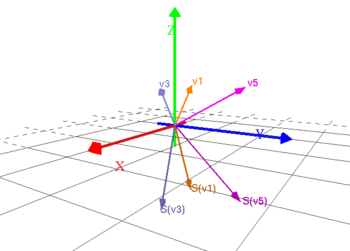
Innan Du börjar arbeta med detta moment så kan Du visualisera spegling i ett plan genom att klicka på bilden.

Övningar

17.10. Låt \displaystyle \underline{\boldsymbol{e}}=\{\boldsymbol{e}_1, \boldsymbol{e}_2\} vara en ON-bas i planet. Bestäm matrisen i basen \displaystyle \underline{\boldsymbol{e}} för följande linjära avbildningar:

1. spegling i \displaystyle x_1-axeln.
2. ortogonal projektion på linjen \displaystyle x_1+x_2=0.
3. spegling i linjen \displaystyle x_1+x_2=0.
4. ortogonal projektion på linjen \displaystyle 4x_1+3x_2=0.

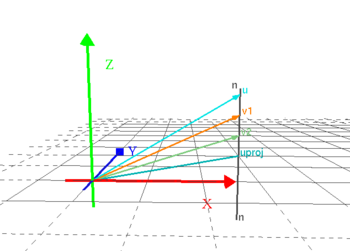
17.11. Låt \displaystyle G vara ortogonal projektion på normalen till planet \displaystyle x_1+x_2+x_3=0 i \displaystyle {\bf E}^3. Ange \displaystyle G:s matris i standardbasen. (Jämför med Övning 13.18a och Exempel 16.19)

17.12. Låt \displaystyle F vara ortogonal projektion på planet \displaystyle x_1+x_2+x_3=0 i \displaystyle {\bf E}^3. Ange \displaystyle F:s matris i standardbasen. (Jämför med Övning 13.18b och Exempel 16.14)

17.13. Låt \displaystyle F vara spegling i planet \displaystyle x_1+x_2+x_3=0 i \displaystyle {\bf E}^3. Ange \displaystyle F:s matris i standardbasen.

17.14. Låt \displaystyle W=[(2,-2,1)^t,(2,1,-2)^t] i \displaystyle {\bf E}^3. Bestäm matrisen för speglingen \displaystyle S i \displaystyle W.

17.15. Låt \displaystyle W=[(1,1,1,1)^t,(1,-1,1,-1)^t] i \displaystyle {\bf E}^4. Bestäm matrisen för den ortogonala projektionen \displaystyle F på \displaystyle W, dvs projektion på \displaystyle W parallellt med \displaystyle W^{\perp}.

17.16. Låt \displaystyle W=\{\boldsymbol{x}\in\bf{ E}^4:\ x_1+x_2+x_3+x_4=0\}. Bestäm matrisen för den ortogonala projektionen \displaystyle P på \displaystyle W.

Innan Du börjar arbeta med detta moment så kan Du bestämma matrisen för en ortogonal projektion genom att klicka på bilden.

Innan Du börjar arbeta med detta moment så kan Du bestämma matrisen för en spegling genom att klicka på bilden.

<imagemap>: bilden är ogiltig eller existerar inte

Reflektionsuppgifter

1. Tänk igenom hur du kan pröva de olika svaren du fått fram på uppgifterna.

2. Genomför ngn/några prövningar

3. Försök att skriva ner eller förklara för en kamrat de olika principerna du använt för att ta fram avbildningarnas matriser.