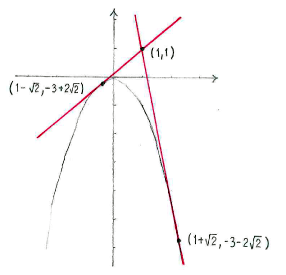
Lösung 1.1:5
Aus Online Mathematik Brückenkurs 2
Suppose that the tangent touches the curve at the point \displaystyle \left( x_{0} \right.,\left. y_{0} \right). That point must, first and foremost, lie on the curve and therefore satisfy the equation of the curve, i.e.
\displaystyle y_{0}=-x_{0}^{2}\quad \quad \quad \left( 1 \right)
If we now write the equation of the tangent as
\displaystyle y=kx+m, the gradient of the tangent,
\displaystyle k, is given by the value of the curve's derivative,
\displaystyle {y}'=-2x, at
\displaystyle x=x_{0},
\displaystyle k=-2x_{0}\quad \quad \quad \left( 2 \right)
The condition that the tangent goes through the point \displaystyle \left( x_{0} \right.,\left. y_{0} \right) gives us that
\displaystyle y_{0}=k\centerdot x_{0}+m\quad \quad \quad \left( 3 \right)
In addition to this, the tangent should also pass through the point
\displaystyle \left( 1 \right.,\left. 1 \right),
\displaystyle 1=k\centerdot 1+m\quad \quad \quad \left( 4 \right)
Equations (1)-(4) constitute an equation system in the unknowns
\displaystyle x_{0},\ y_{0},\ k
and
\displaystyle m.
Because we are looking for \displaystyle x_{0}\text{ } and \displaystyle y_{0}, the first step is to try and eliminate \displaystyle k and \displaystyle m from the equations.
Equation (2) gives that \displaystyle k=-\text{2 }x_{0} and substituting this into equation (4) gives
\displaystyle 1=-2x_{0}+m\quad \Leftrightarrow \quad m=2x_{0}+1
With \displaystyle k and \displaystyle m expressed in terms of \displaystyle x_{0} and \displaystyle y_{0}, (3) becomes an equation that is expressed completely in terms of \displaystyle x_{0} and \displaystyle y_{0},
\displaystyle y_{0}=-2x_{0}^{2}+2x_{0}+1\quad \quad \quad \left( 3' \right)
This equation, together with (1), is an equation system in
\displaystyle x_{0}
and
\displaystyle y_{0}
\displaystyle \left\{ \begin{array}{*{35}l} y_{0}=-x_{0}^{2} \\ y_{0}=-2x_{0}^{2}+2x_{0}+1 \\ \end{array} \right.
Substituting equation (1) into (3') gives us an equation in x0,
\displaystyle -x_{0}^{2}=-2x_{0}^{2}+2x_{0}+1
i.e.
\displaystyle x_{0}^{2}-2x_{0}-1=0
This second-degree equation has solutions
\displaystyle x_{0}=1-\sqrt{2}
and
\displaystyle x_{0}=1+\sqrt{2}
Equation (1) gives the corresponding y-values:
\displaystyle y_{0}=-3+2\sqrt{2}
and
\displaystyle y_{0}=-3-2\sqrt{2}
Thus, the answers are the points
\displaystyle \left( 1-\sqrt{2} \right.,\left. -3+2\sqrt{2} \right)
and
\displaystyle \left( 1+\sqrt{2} \right.,\left. -3-2\sqrt{2} \right).