Lösung 1.1:5

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
Suppose that the tangent touches the curve at the point <math>(x_0,y_0)</math>. That point must, first and foremost, lie on the curve and therefore satisfy the equation of the curve, i.e.
Suppose that the tangent touches the curve at the point <math>(x_0,y_0)</math>. That point must, first and foremost, lie on the curve and therefore satisfy the equation of the curve, i.e.
-
{{Displayed math||<math>y_0 = -x_0^2\,\textrm{.}</math>|(1)}}
+
{{Abgesetzte Formel||<math>y_0 = -x_0^2\,\textrm{.}</math>|(1)}}
If we now write the equation of the tangent as <math>y=kx+m</math>, the slope of the tangent, ''k'', is given by the value of the curve's derivative, <math>y^{\,\prime} = -2x</math>, at <math>x=x_0</math>,
If we now write the equation of the tangent as <math>y=kx+m</math>, the slope of the tangent, ''k'', is given by the value of the curve's derivative, <math>y^{\,\prime} = -2x</math>, at <math>x=x_0</math>,
-
{{Displayed math||<math>k = -2x_0\,\textrm{.}</math>|(2)}}
+
{{Abgesetzte Formel||<math>k = -2x_0\,\textrm{.}</math>|(2)}}
The condition that the tangent goes through the point <math>(x_0,y_0)</math> gives us that
The condition that the tangent goes through the point <math>(x_0,y_0)</math> gives us that
-
{{Displayed math||<math>y_{0} = k\cdot x_0 + m\,\textrm{.}</math>|(3)}}
+
{{Abgesetzte Formel||<math>y_{0} = k\cdot x_0 + m\,\textrm{.}</math>|(3)}}
In addition to this, the tangent should also pass through the point (1,1),
In addition to this, the tangent should also pass through the point (1,1),
-
{{Displayed math||<math>1 = k\cdot 1 + m\,\textrm{.}</math>|(4)}}
+
{{Abgesetzte Formel||<math>1 = k\cdot 1 + m\,\textrm{.}</math>|(4)}}
Equations (1)-(4) constitute a system of equations in the unknowns <math>x_0</math>, <math>y_{0}</math>, <math>k</math> and <math>m</math>.
Equations (1)-(4) constitute a system of equations in the unknowns <math>x_0</math>, <math>y_{0}</math>, <math>k</math> and <math>m</math>.
Zeile 21: Zeile 21:
Equation (2) gives that <math>k = -2 x_0</math> and substituting this into equation (4) gives
Equation (2) gives that <math>k = -2 x_0</math> and substituting this into equation (4) gives
-
{{Displayed math||<math>1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.}</math>}}
With ''k'' and ''m'' expressed in terms of <math>x_0</math> and <math>y_0</math>, (3) becomes an equation that is expressed completely in terms of <math>x_0</math>
With ''k'' and ''m'' expressed in terms of <math>x_0</math> and <math>y_0</math>, (3) becomes an equation that is expressed completely in terms of <math>x_0</math>
and <math>y_0</math>,
and <math>y_0</math>,
-
{{Displayed math||<math>y_0 = -2x_0^2 + 2x_0 + 1\,\textrm{.}</math>|(3')}}
+
{{Abgesetzte Formel||<math>y_0 = -2x_0^2 + 2x_0 + 1\,\textrm{.}</math>|(3')}}
This equation, together with (1), is a system of equations in <math>x_0</math> and <math>y_0</math>,
This equation, together with (1), is a system of equations in <math>x_0</math> and <math>y_0</math>,
-
{{Displayed math||<math>\left\{\begin{align}
+
{{Abgesetzte Formel||<math>\left\{\begin{align}
y_{0} &= -x_0^{2}\,,\\[5pt]
y_{0} &= -x_0^{2}\,,\\[5pt]
y_{0} &= -2x_0^2 + 2x_0 + 1\,\textrm{.}
y_{0} &= -2x_0^2 + 2x_0 + 1\,\textrm{.}
Zeile 37: Zeile 37:
Substituting equation (1) into (3') gives us an equation in <math>x_0</math>,
Substituting equation (1) into (3') gives us an equation in <math>x_0</math>,
-
{{Displayed math||<math>-x_0^2 = -2x_0^2 + 2x_0 + 1\,,</math>}}
+
{{Abgesetzte Formel||<math>-x_0^2 = -2x_0^2 + 2x_0 + 1\,,</math>}}
i.e.
i.e.
-
{{Displayed math||<math>x_0^2 - 2x_0 - 1 = 0\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x_0^2 - 2x_0 - 1 = 0\,\textrm{.}</math>}}
This quadratic equation has solutions
This quadratic equation has solutions
-
{{Displayed math||<math>x_0 = 1-\sqrt{2}\qquad\text{and}\qquad x_0 = 1+\sqrt{2}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>x_0 = 1-\sqrt{2}\qquad\text{and}\qquad x_0 = 1+\sqrt{2}\,\textrm{.}</math>}}
Equation (1) gives the corresponding y-values,
Equation (1) gives the corresponding y-values,
-
{{Displayed math||<math>y_0 = -3+2\sqrt{2}\qquad\text{and}\qquad y_0 = -3-2\sqrt{2}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>y_0 = -3+2\sqrt{2}\qquad\text{and}\qquad y_0 = -3-2\sqrt{2}\,\textrm{.}</math>}}
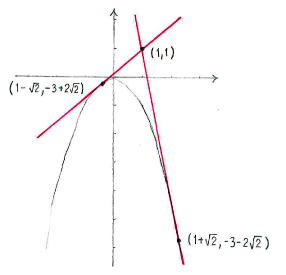
Thus, the answers are the points <math>(1-\sqrt{2},-3+2\sqrt{2})</math> and
Thus, the answers are the points <math>(1-\sqrt{2},-3+2\sqrt{2})</math> and

Version vom 12:51, 10. Mär. 2009

Suppose that the tangent touches the curve at the point \displaystyle (x_0,y_0). That point must, first and foremost, lie on the curve and therefore satisfy the equation of the curve, i.e.

\displaystyle y_0 = -x_0^2\,\textrm{.} (1)

If we now write the equation of the tangent as \displaystyle y=kx+m, the slope of the tangent, k, is given by the value of the curve's derivative, \displaystyle y^{\,\prime} = -2x, at \displaystyle x=x_0,

\displaystyle k = -2x_0\,\textrm{.} (2)

The condition that the tangent goes through the point \displaystyle (x_0,y_0) gives us that

\displaystyle y_{0} = k\cdot x_0 + m\,\textrm{.} (3)

In addition to this, the tangent should also pass through the point (1,1),

\displaystyle 1 = k\cdot 1 + m\,\textrm{.} (4)

Equations (1)-(4) constitute a system of equations in the unknowns \displaystyle x_0, \displaystyle y_{0}, \displaystyle k and \displaystyle m.

Because we are looking for \displaystyle x_0 and \displaystyle y_0, the first step is to try and eliminate k and m from the equations.

Equation (2) gives that \displaystyle k = -2 x_0 and substituting this into equation (4) gives

\displaystyle 1 = -2x_0 + m\quad\Leftrightarrow\quad m = 2x_0+1\,\textrm{.}

With k and m expressed in terms of \displaystyle x_0 and \displaystyle y_0, (3) becomes an equation that is expressed completely in terms of \displaystyle x_0 and \displaystyle y_0,

\displaystyle y_0 = -2x_0^2 + 2x_0 + 1\,\textrm{.} (3')

This equation, together with (1), is a system of equations in \displaystyle x_0 and \displaystyle y_0,

\displaystyle \left\{\begin{align}

y_{0} &= -x_0^{2}\,,\\[5pt] y_{0} &= -2x_0^2 + 2x_0 + 1\,\textrm{.} \end{align}\right.

Substituting equation (1) into (3') gives us an equation in \displaystyle x_0,

\displaystyle -x_0^2 = -2x_0^2 + 2x_0 + 1\,,

i.e.

\displaystyle x_0^2 - 2x_0 - 1 = 0\,\textrm{.}

This quadratic equation has solutions

\displaystyle x_0 = 1-\sqrt{2}\qquad\text{and}\qquad x_0 = 1+\sqrt{2}\,\textrm{.}

Equation (1) gives the corresponding y-values,

\displaystyle y_0 = -3+2\sqrt{2}\qquad\text{and}\qquad y_0 = -3-2\sqrt{2}\,\textrm{.}

Thus, the answers are the points \displaystyle (1-\sqrt{2},-3+2\sqrt{2}) and \displaystyle (1+\sqrt{2},-3-2\sqrt{2})\,.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.1:5“