Lösung 1.1:4
Aus Online Mathematik Brückenkurs 2
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
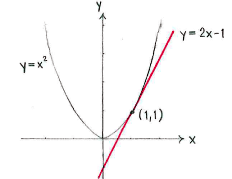
If we write the equation of the tangent as | If we write the equation of the tangent as | ||
| - | {{ | + | {{Abgesetzte Formel||<math>y=kx+m</math>}} |
we know that the tangent's slope ''k'' is equal to the derivative of <math>y = x^2</math> at the point <math>x=1\,</math>, and since <math>y^{\,\prime} = 2x\,</math>, so | we know that the tangent's slope ''k'' is equal to the derivative of <math>y = x^2</math> at the point <math>x=1\,</math>, and since <math>y^{\,\prime} = 2x\,</math>, so | ||
| - | {{ | + | {{Abgesetzte Formel||<math>k = y^{\,\prime}(1) = 2\cdot 1 = 2\,\textrm{.}</math>}} |
We can determine the constant ''m'' with the condition that the tangent should go through the grazing point (1,1), i.e. the point (1,1) should satisfy the equation of the tangent | We can determine the constant ''m'' with the condition that the tangent should go through the grazing point (1,1), i.e. the point (1,1) should satisfy the equation of the tangent | ||
| - | {{ | + | {{Abgesetzte Formel||<math>1 = 2\cdot 1 + m</math>}} |
which gives that <math>m=-1</math>. | which gives that <math>m=-1</math>. | ||
| Zeile 19: | Zeile 19: | ||
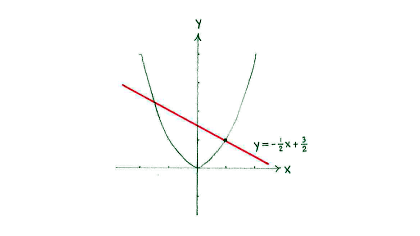
Because two straight lines which are perpendicular to each other have slopes which satisfy <math>k_{1}\cdot k_{2} = -1\,</math>, the normal must have a slope which is equal to | Because two straight lines which are perpendicular to each other have slopes which satisfy <math>k_{1}\cdot k_{2} = -1\,</math>, the normal must have a slope which is equal to | ||
| - | {{ | + | {{Abgesetzte Formel||<math>-\frac{1}{k} = -\frac{1}{2}\,\textrm{.}</math>}} |
The equation of the normal can therefore be written as | The equation of the normal can therefore be written as | ||
| - | {{ | + | {{Abgesetzte Formel||<math>y=-\frac{1}{2}x+n</math>}} |
where ''n'' is some constant. | where ''n'' is some constant. | ||
| Zeile 29: | Zeile 29: | ||
Since the normal must pass through the line (1,1), we can determine the constant ''n'' if we substitute the point into the equation of the normal, | Since the normal must pass through the line (1,1), we can determine the constant ''n'' if we substitute the point into the equation of the normal, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>1=-\frac{1}{2}\cdot + n</math>}} |
and this gives <math>n=\tfrac{3}{2}\,</math>. | and this gives <math>n=\tfrac{3}{2}\,</math>. | ||
[[Image:1_1_4-3(3).gif|center]] | [[Image:1_1_4-3(3).gif|center]] | ||
Version vom 12:51, 10. Mär. 2009
If we write the equation of the tangent as
| \displaystyle y=kx+m |
we know that the tangent's slope k is equal to the derivative of \displaystyle y = x^2 at the point \displaystyle x=1\,, and since \displaystyle y^{\,\prime} = 2x\,, so
| \displaystyle k = y^{\,\prime}(1) = 2\cdot 1 = 2\,\textrm{.} |
We can determine the constant m with the condition that the tangent should go through the grazing point (1,1), i.e. the point (1,1) should satisfy the equation of the tangent
| \displaystyle 1 = 2\cdot 1 + m |
which gives that \displaystyle m=-1.
The normal to the curve \displaystyle y=x^2 at the point (1,1) is the straight line which is perpendicular to the tangent at the same point.
Because two straight lines which are perpendicular to each other have slopes which satisfy \displaystyle k_{1}\cdot k_{2} = -1\,, the normal must have a slope which is equal to
| \displaystyle -\frac{1}{k} = -\frac{1}{2}\,\textrm{.} |
The equation of the normal can therefore be written as
| \displaystyle y=-\frac{1}{2}x+n |
where n is some constant.
Since the normal must pass through the line (1,1), we can determine the constant n if we substitute the point into the equation of the normal,
| \displaystyle 1=-\frac{1}{2}\cdot + n |
and this gives \displaystyle n=\tfrac{3}{2}\,.