Lösung 1.1:4
Aus Online Mathematik Brückenkurs 2
K (Lösning 1.1:4 moved to Solution 1.1:4: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | {{ | + | If we write the equation of the tangent as |
| - | < | + | |
| - | < | + | |
| - | < | + | <math>y=kx+m</math> |
| - | { | + | |
| + | |||
| + | we know that the tangent's gradient | ||
| + | <math>k</math> | ||
| + | is equal to the derivative of | ||
| + | <math>y=x^{\text{2}}\text{ }</math> | ||
| + | at the point | ||
| + | <math>x=\text{1}</math>, and since | ||
| + | |||
| + | <math>{y}'=\text{2}x</math>, so | ||
| + | |||
| + | |||
| + | <math>k={y}'\left( 1 \right)=2\centerdot 1=2</math> | ||
| + | |||
| + | We can determine the constant | ||
| + | <math>m\text{ }</math> | ||
| + | with the condition that the tangent should go through the grazing point | ||
| + | <math>\left( 1 \right.,\left. 1 \right)</math>, i.e. the point | ||
| + | <math>\left( 1 \right.,\left. 1 \right)</math> | ||
| + | should satisfy the equation of the tangent | ||
| + | |||
| + | |||
| + | <math>1=2\centerdot 1+m</math> | ||
| + | |||
| + | |||
| + | which gives that | ||
| + | <math>m=-\text{1}</math> | ||
[[Image:1_1_4_1.gif|center]] | [[Image:1_1_4_1.gif|center]] | ||
| + | |||
| + | |||
| + | The normal to the curve | ||
| + | <math>y=x^{\text{2}}\text{ }</math> | ||
| + | at the point | ||
| + | <math>\left( 1 \right.,\left. 1 \right)</math> | ||
| + | is the straight line which is perpendicular to the tangent at the same point. | ||
| + | |||
| + | Because two straight lines which are perpendicular to each other have gradients which satisfy | ||
| + | <math>k_{1}\centerdot k_{2}=-1</math>, the normal must have a gradient which is equal to | ||
| + | |||
| + | |||
| + | <math>-\frac{1}{k}=-\frac{1}{2}</math> | ||
| + | |||
| + | |||
| + | The equation of the normal can therefore be written as | ||
| + | |||
| + | |||
| + | <math>y=-\frac{1}{2}x+n</math> | ||
| + | |||
| + | |||
| + | where | ||
| + | <math>n</math> | ||
| + | is some constant. | ||
| + | |||
| + | Since the normal must pass through the line | ||
| + | <math>\left( 1 \right.,\left. 1 \right)</math>, we can determine the constant | ||
| + | <math>n</math> | ||
| + | if we substitute the point into the equation of the normal, | ||
| + | |||
| + | |||
| + | <math>1=-\frac{1}{2}\centerdot +n</math> | ||
| + | |||
| + | |||
| + | and this gives | ||
| + | <math>n=\frac{3}{2}</math>. | ||
| + | |||
| + | |||
| + | |||
[[Image:1_1_4-3(3).gif|center]] | [[Image:1_1_4-3(3).gif|center]] | ||
Version vom 12:12, 10. Okt. 2008
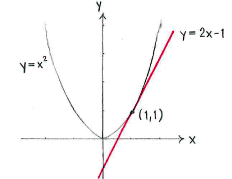
If we write the equation of the tangent as
\displaystyle y=kx+m
we know that the tangent's gradient
\displaystyle k
is equal to the derivative of
\displaystyle y=x^{\text{2}}\text{ }
at the point
\displaystyle x=\text{1}, and since
\displaystyle {y}'=\text{2}x, so
\displaystyle k={y}'\left( 1 \right)=2\centerdot 1=2
We can determine the constant \displaystyle m\text{ } with the condition that the tangent should go through the grazing point \displaystyle \left( 1 \right.,\left. 1 \right), i.e. the point \displaystyle \left( 1 \right.,\left. 1 \right) should satisfy the equation of the tangent
\displaystyle 1=2\centerdot 1+m
which gives that
\displaystyle m=-\text{1}
The normal to the curve
\displaystyle y=x^{\text{2}}\text{ }
at the point
\displaystyle \left( 1 \right.,\left. 1 \right)
is the straight line which is perpendicular to the tangent at the same point.
Because two straight lines which are perpendicular to each other have gradients which satisfy \displaystyle k_{1}\centerdot k_{2}=-1, the normal must have a gradient which is equal to
\displaystyle -\frac{1}{k}=-\frac{1}{2}
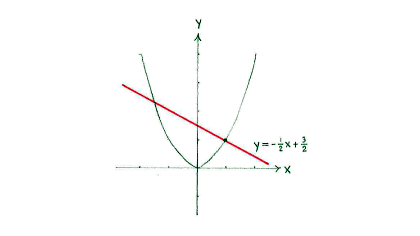
The equation of the normal can therefore be written as
\displaystyle y=-\frac{1}{2}x+n
where
\displaystyle n
is some constant.
Since the normal must pass through the line \displaystyle \left( 1 \right.,\left. 1 \right), we can determine the constant \displaystyle n if we substitute the point into the equation of the normal,
\displaystyle 1=-\frac{1}{2}\centerdot +n
and this gives
\displaystyle n=\frac{3}{2}.