Lösung 1.1:4

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 1.1:4 moved to Solution 1.1:4: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
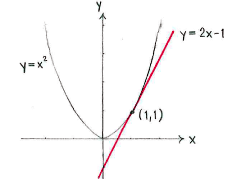
If we write the equation of the tangent as
-
<center> [[Image:1_1_4-1(3).gif]] </center>
+
 
-
<center> [[Image:1_1_4-2(3).gif]] </center>
+
 
-
<center> [[Image:1_1_4-3(3).gif]] </center>
+
<math>y=kx+m</math>
-
{{NAVCONTENT_STOP}}
+
 
 +
 
 +
we know that the tangent's gradient
 +
<math>k</math>
 +
is equal to the derivative of
 +
<math>y=x^{\text{2}}\text{ }</math>
 +
at the point
 +
<math>x=\text{1}</math>, and since
 +
 
 +
<math>{y}'=\text{2}x</math>, so
 +
 
 +
 
 +
<math>k={y}'\left( 1 \right)=2\centerdot 1=2</math>
 +
 
 +
We can determine the constant
 +
<math>m\text{ }</math>
 +
with the condition that the tangent should go through the grazing point
 +
<math>\left( 1 \right.,\left. 1 \right)</math>, i.e. the point
 +
<math>\left( 1 \right.,\left. 1 \right)</math>
 +
should satisfy the equation of the tangent
 +
 
 +
 
 +
<math>1=2\centerdot 1+m</math>
 +
 
 +
 
 +
which gives that
 +
<math>m=-\text{1}</math>
[[Image:1_1_4_1.gif|center]]
[[Image:1_1_4_1.gif|center]]
 +
 +
 +
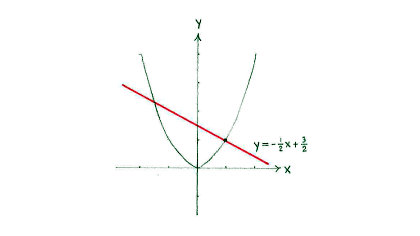
The normal to the curve
 +
<math>y=x^{\text{2}}\text{ }</math>
 +
at the point
 +
<math>\left( 1 \right.,\left. 1 \right)</math>
 +
is the straight line which is perpendicular to the tangent at the same point.
 +
 +
Because two straight lines which are perpendicular to each other have gradients which satisfy
 +
<math>k_{1}\centerdot k_{2}=-1</math>, the normal must have a gradient which is equal to
 +
 +
 +
<math>-\frac{1}{k}=-\frac{1}{2}</math>
 +
 +
 +
The equation of the normal can therefore be written as
 +
 +
 +
<math>y=-\frac{1}{2}x+n</math>
 +
 +
 +
where
 +
<math>n</math>
 +
is some constant.
 +
 +
Since the normal must pass through the line
 +
<math>\left( 1 \right.,\left. 1 \right)</math>, we can determine the constant
 +
<math>n</math>
 +
if we substitute the point into the equation of the normal,
 +
 +
 +
<math>1=-\frac{1}{2}\centerdot +n</math>
 +
 +
 +
and this gives
 +
<math>n=\frac{3}{2}</math>.
 +
 +
 +
[[Image:1_1_4-3(3).gif|center]]
[[Image:1_1_4-3(3).gif|center]]

Version vom 12:12, 10. Okt. 2008

If we write the equation of the tangent as


\displaystyle y=kx+m


we know that the tangent's gradient \displaystyle k is equal to the derivative of \displaystyle y=x^{\text{2}}\text{ } at the point \displaystyle x=\text{1}, and since

\displaystyle {y}'=\text{2}x, so


\displaystyle k={y}'\left( 1 \right)=2\centerdot 1=2

We can determine the constant \displaystyle m\text{ } with the condition that the tangent should go through the grazing point \displaystyle \left( 1 \right.,\left. 1 \right), i.e. the point \displaystyle \left( 1 \right.,\left. 1 \right) should satisfy the equation of the tangent


\displaystyle 1=2\centerdot 1+m


which gives that \displaystyle m=-\text{1}



The normal to the curve \displaystyle y=x^{\text{2}}\text{ } at the point \displaystyle \left( 1 \right.,\left. 1 \right) is the straight line which is perpendicular to the tangent at the same point.

Because two straight lines which are perpendicular to each other have gradients which satisfy \displaystyle k_{1}\centerdot k_{2}=-1, the normal must have a gradient which is equal to


\displaystyle -\frac{1}{k}=-\frac{1}{2}


The equation of the normal can therefore be written as


\displaystyle y=-\frac{1}{2}x+n


where \displaystyle n is some constant.

Since the normal must pass through the line \displaystyle \left( 1 \right.,\left. 1 \right), we can determine the constant \displaystyle n if we substitute the point into the equation of the normal,


\displaystyle 1=-\frac{1}{2}\centerdot +n


and this gives \displaystyle n=\frac{3}{2}.


Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.1:4“