Lösung 1.1:1a

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Lösning 1.1:1a moved to Solution 1.1:1a: Robot: moved page)
Zeile 1: Zeile 1:
-
{{NAVCONTENT_START}}
+
The derivative
-
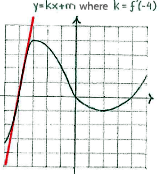
The derivative f'(-4)gives the function's instantaneous rate of change at the point x=-4, i.e. it is a measure of the function's value changes in the vicinity of x=-4.
+
<math>{f}'\left( -4 \right)</math>
 +
gives the function's instantaneous rate of change at the point
 +
<math>x=-\text{4}</math>, i.e. it is a measure of the function's value changes in the vicinity of
 +
<math>x=-\text{4}</math>.
 +
 
 +
In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point
 +
<math>x=-\text{4}</math>.
 +
 +
 
-
In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point x=-4.
 
[[Image:1_1_1_a1.gif|center]]
[[Image:1_1_1_a1.gif|center]]
-
Because the tangent is sloping upwards, it has a positive gradient and therefore f'(-4)>0.
+
<math>y=kx+m\text{ }</math>
 +
where
 +
<math>k={f}'\left( -\text{4} \right)</math>
 +
 
 +
 
 +
Because the tangent is sloping upwards, it has a positive gradient and therefore
 +
<math>{f}'\left( -\text{4} \right)>0</math>.
-
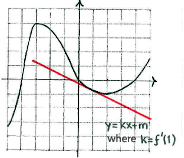
At the point x=1, the tangent slopes downwards and this means that f'(1)<0.
+
At the point
 +
<math>x=\text{1}</math>, the tangent slopes downwards and this means that
 +
<math>{f}'\left( \text{1} \right)<0</math>.
[[Image:1_1_1_a2.gif|center]]
[[Image:1_1_1_a2.gif|center]]
-
{{NAVCONTENT_STOP}}
+
<math>y=kx+m\text{ }</math>
 +
where
 +
<math>k={f}'\left( 1 \right)</math>

Version vom 11:11, 10. Okt. 2008

The derivative \displaystyle {f}'\left( -4 \right) gives the function's instantaneous rate of change at the point \displaystyle x=-\text{4}, i.e. it is a measure of the function's value changes in the vicinity of \displaystyle x=-\text{4}.

In the graph of the function, this derivative is equal to the slope of the tangent to the curve of function at the point \displaystyle x=-\text{4}.



\displaystyle y=kx+m\text{ } where \displaystyle k={f}'\left( -\text{4} \right)


Because the tangent is sloping upwards, it has a positive gradient and therefore \displaystyle {f}'\left( -\text{4} \right)>0.

At the point \displaystyle x=\text{1}, the tangent slopes downwards and this means that \displaystyle {f}'\left( \text{1} \right)<0.

\displaystyle y=kx+m\text{ } where \displaystyle k={f}'\left( 1 \right)

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.1:1a“