Lösung 3.3:1b
Aus Online Mathematik Brückenkurs 2
Zuerst bringen wir \displaystyle \frac{1}{2}+i\frac{\sqrt{3}}{2} in Polarform.
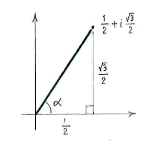
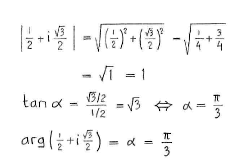
Daher ist
| \displaystyle \frac{1}{2}+i\frac{\sqrt{3}}{2} = 1\cdot \Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr) |
und durch den Moivreschen Satz erhalten wir
| \displaystyle \begin{align}
\Bigl(\frac{1}{2}+i\frac{\sqrt{3}}{2}\Bigr)^{12} &= 1^{12}\cdot\Bigl(\cos\Bigl(12\cdot\frac{\pi}{3}\Bigr) + i\sin\Bigl(12\cdot\frac{\pi}{3}\Bigr)\Bigr)\\[5pt] &= 1\cdot (\cos 4\pi + i\sin 4\pi)\\[5pt] &= 1\cdot (1+i\cdot 0)\\[5pt] &= 1\,\textrm{.} \end{align} |
