10.4 Linjära höljet
SamverkanLinalgLIU
| Rad 15: | Rad 15: | ||
Du har nu läst definitionen av linjära höljet och här kommer några övningar som testar om du har tagit till dig stoffet. | Du har nu läst definitionen av linjära höljet och här kommer några övningar som testar om du har tagit till dig stoffet. | ||
| + | |||
| + | |||
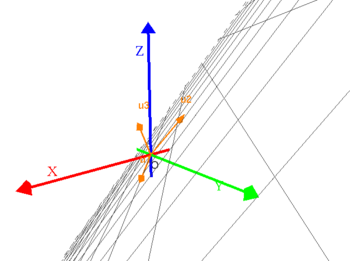
| + | '''''Innan Du börjar arbeta med detta moment så kan Du visualisera linjära höljet genom att klicka på bilden.''''' | ||
| + | |||
| + | <imagemap> | ||
| + | Bild:LinearSpan.png|350px|alt=Alt text | ||
| + | default [http://webcourses.itn.liu.se/webkurs/LinearSpan.jnlp Du kan visualisera linjära höljet] | ||
| + | </imagemap> | ||
| + | |||
Versionen från 12 september 2011 kl. 13.29
| 10.1 | 10.2 | 10.3 | 10.4 | 10.5 | 10.6 | 10.7 |
Läs textavsnitt 10.4 Definition av linjära höljet.
Du har nu läst definitionen av linjära höljet och här kommer några övningar som testar om du har tagit till dig stoffet.
Innan Du börjar arbeta med detta moment så kan Du visualisera linjära höljet genom att klicka på bilden.
Innehåll |
Övning 11.4
Låt \displaystyle M vara mängden i Övning 11.3 och låt \displaystyle U=[M] vara linjära höljet för \displaystyle M , dvs \displaystyle U är mängden av alla linjära kombinationer i \displaystyle M .
a) Ange en ekvation \displaystyle U . Vad kallas den geometriska tolkningen av \displaystyle U .
b) Visa att \displaystyle U är ett underrum.
c) Bestäm alla vektorer som inte ligger i \displaystyle U .
Övning 11.5
Låt
V=[(1,0,0,-1)^t,(0,1,-1,0)^t,(1,1,0,0)^t]
och
W=[(1,0,0,-1)^t,(0,1,-1,0)^t,(1,0,0,1)^t].
a) Ange en ekvation för \displaystyle V resp. \displaystyle W .
b) Låt mängden \displaystyle U vara som i Övning 10.4. Bestäm snittmängden \displaystyle U\cap V , dvs mängden av alla gemensamma vektorer som ligger i både \displaystyle U och \displaystyle V . Bestäm också \displaystyle U\cap W .

 Hämtar...
Hämtar...