2. Introduktion till krafter och gravitation
Förberedande Mekanik
| Theory | Exercises |
Grundbegrepp
Newtons första lag
En partikel förblir i vila eller rör sig rakt fram med konstant hastighet, om resultanten på den är noll.
Jämvikt
Om resultanten på en partikel är noll, sägs krafterna som verkar på den stå i jämvikt.
Den universalla gravitationslagen
| \displaystyle F=\frac{Gm_{1}m_{2}}{{d}^{\ 2}}
\displaystyle G=6\textrm{.}67\times 10^{-11}\text{ kg}^{\text{-1}}\text{m}^{\text{3}}\text{s}^{\text{-2}} | 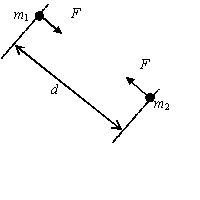
|
Gravitationen på jorden
Gravitationskraften kallas ofta för vikt.
\displaystyle \begin{align} & F=mg \\ & g=9\textrm{.}8\text{ ms}^{\text{-2}} \\ \end{align}
Några data
Jordens radie är \displaystyle \text{6}\textrm{.}\text{37}\times \text{1}0^{\text{6}}\text{ } meter.
Jordens massa är \displaystyle \text{5}\textrm{.}\text{98}\times \text{1}0^{\text{24}}\text{ } kg.
Exempel
Avgör om krafterna som verkar på följande objekt står i jämvikt eller ej.
a) En resande i ett tåg som åker med konstant hastighet.
b) En het luftballong som stiger med konstant fart.
c) En sten som släpps i en mycket djup schakt full med vatten.
Lösning
a) Ja, om tåget åker på en rätlinjig bana.
b) Ja, om ballongen stiger exakt rakt upp.
c) Ja, när stenen når en sluthastighet som är konstant längs en rätlinjig bana.
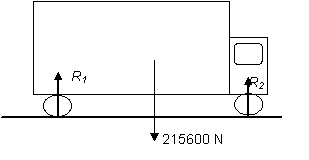
Hur stor är gravitationskraften (vikten) som verkar på en lastbil med en massa på 22 ton.
Lösning
Beräkningen är gjord med enheten \displaystyle mg för vikt.
\displaystyle \begin{align} & mg=22000\times 9\textrm{.}8 \\ & =215600\text{ N} \end{align}
Bilden visar lastbilen och dess vikt.
Beakta att även reaktionskrafter verkar uppåt på varje hjul.
\displaystyle {{R}_{1}}+{{R}_{2}}+{{R}_{3}}+{{R}_{4}}=215600\ \text{N}
En låda med massan 30 kg ligger på ett bord.
a) Beräkna lådans vikt.
b) Ange storleken på den uppåt riktade kraft som bordet utövar på lådan.
Lösning
a)
\displaystyle \begin{align} & W=30\times 9\textrm{.}8 \\ & =294\text{ N} \end{align}
b) En kraft på 294 N måste verka på lådan för att den ska vara i jämvikt.
En satellit med massan 400 kg är på en höjd av 12 km över jordytan. Hur stor är gravitationskraften som verkar på satelliten?
Data: \displaystyle G=6\textrm{.}67\times {{10}^{-11}} \displaystyle \text{k}{{\text{g}}^{-\text{1}}}{{\text{m}}^{\text{3}}}{{\text{s}}^{-\text{2}}}
Jordradien \displaystyle =6\textrm{.}37\times {{10}^{6}} \text{m}
Jordens massa \displaystyle =5\textrm{.}98\times {{10}^{24}} \text{kg}
Lösning
\displaystyle \begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ {2}}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 400\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 6\textrm{.}37\times {{10}^{6}}+12000 \right)}^{2}}} \\ & =3917\text{ N} \end{align}
Solen har massan \displaystyle 1\textrm{.}99\times {{10}^{30}} \text{kg} . The mean distance of the earth from the sun is approximately \displaystyle 1\textrm{.}5\times {{10}^{11}} \text{m} .
(a) Beräkna den kraft som solen utövar på jorden.
(b) Beräkna den kraft som jorden utövar på solen.
(c) Förklara varför denna kraft varierar.
Lösning
(a)
\displaystyle \begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ 2}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 1\textrm{.}99\times {{10}^{30}}\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 1\textrm{.}5\times {{10}^{11}} \right)}^{2}}} \\ & =3\textrm{.}53\times {{10}^{22}}\text{ N} \end{align}
(b) \displaystyle 3\textrm{.}53\times {{10}^{22}}\text{ N}
(c) Avståndet mellan jorden och solen varierar.