Förberedande Mekanik

Theory

Exercises

Grundbegrepp

Newtons första lag

En partikel förblir i vila eller rör sig rakt fram med konstant hastighet, om resultanten på den är noll.

Jämvikt

Om resultanten på en partikel är noll, sägs krafterna som verkar på den stå i jämvikt.

Den universalla gravitationslagen

\displaystyle F=\frac{Gm_{1}m_{2}}{{d}^{\ 2}} \displaystyle G=6\textrm{.}67\times 10^{-11}\text{ kg}^{\text{-1}}\text{m}^{\text{3}}\text{s}^{\text{-2}}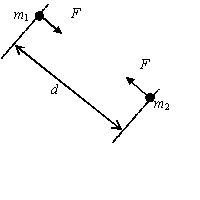

Gravitationen på jorden

Gravitationskraften kallas ofta för vikt.

\displaystyle \begin{align} & F=mg \\ & g=9\textrm{.}8\text{ ms}^{\text{-2}} \\ \end{align}

Några data

Jordens radie är \displaystyle \text{6}\textrm{.}\text{37}\times \text{1}0^{\text{6}}\text{ } meter.

Jordens massa är \displaystyle \text{5}\textrm{.}\text{98}\times \text{1}0^{\text{24}}\text{ } kg.

Exempel

Exempel 2.1

Avgör om krafterna som verkar på följande objekt står i jämvikt eller ej.

a) En resande i ett tåg som åker med konstant hastighet.

b) En het luftballong som stiger med konstant fart.

c) En sten som släpps i en mycket djup schakt full med vatten.

Solution 2.1

a) Ja, om tåget åker på en rätlinjig bana.

b) Ja, om ballongen stiger exakt rakt upp.

c) Ja, om stenen når ett tillstånd så att den sjunker med konstant hastighet längs en rätlinjig bana.

Example 2.2

Find the magnitude of the force of gravity (weight) acting on a lorry of mass 22 tonnes.

Solution

This is calculated using the fact that the weight is given by \displaystyle mg.

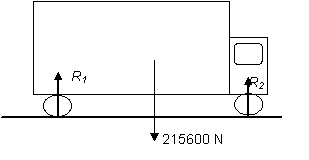
\displaystyle \begin{align} & mg=22000\times 9\textrm{.}8 \\ & =215600\text{ N} \end{align}

The diagram shows the lorry and its weight.

Note that reaction forces also act upwards on each wheel.

\displaystyle {{R}_{1}}+{{R}_{2}}+{{R}_{3}}+{{R}_{4}}=215600\ \text{N}

Example 2.3

A box of mass 30 kg is at rest on a table.

a) Calculate the weight of the box.

b) State the magnitude of the upward force that the table exerts on the box.

Solution

a)

\displaystyle \begin{align} & W=30\times 9\textrm{.}8 \\ & =294\text{ N} \end{align}

b) An upward force of 294 N must act for the box to remain in equilibrium.

Example 2.4

A satellite, of mass 400 kg, is at a height of 12 km above the surface of the earth. Find the magnitude of the gravitational attraction on the satellite.

Data: \displaystyle G=6\textrm{.}67\times {{10}^{-11}} \displaystyle \text{k}{{\text{g}}^{-\text{1}}}{{\text{m}}^{\text{3}}}{{\text{s}}^{-\text{2}}}

Radius of earth \displaystyle =6\textrm{.}37\times {{10}^{6}} \text{m}

Mass of earth \displaystyle =5\textrm{.}98\times {{10}^{24}} \text{kg}

Solution

\displaystyle \begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ {2}}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 400\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 6\textrm{.}37\times {{10}^{6}}+12000 \right)}^{2}}} \\ & =3917\text{ N} \end{align}

Example 2.5

The sun has mass \displaystyle 1\textrm{.}99\times {{10}^{30}} \text{kg} . The mean distance of the earth from the sun is approximately \displaystyle 1\textrm{.}5\times {{10}^{11}} \text{m} .

(a) Calculate the force that the sun exerts on the earth.

(b) State the force that the earth exerts on the sun.

(c) Explain why this force varies.

Solution

(a)

\displaystyle \begin{align} & \frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{\ 2}}}=\frac{6\textrm{.}67\times {{10}^{-11}}\times 1\textrm{.}99\times {{10}^{30}}\times 5\textrm{.}98\times {{10}^{24}}}{{{\left( 1\textrm{.}5\times {{10}^{11}} \right)}^{2}}} \\ & =3\textrm{.}53\times {{10}^{22}}\text{ N} \end{align}

(b) \displaystyle 3\textrm{.}53\times {{10}^{22}}\text{ N}

(c) The distance between the earth and the sun varies.