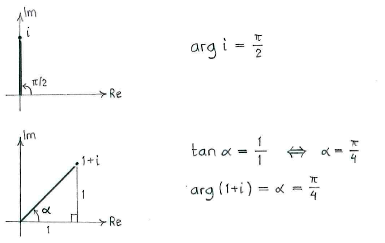Lösung 3.2:5d
Aus Online Mathematik Brückenkurs 2
Wenn wir eine komplexe Zahl durch eine andere dividieren, subtrahieren wir das Argument des Nenners vom Argument des Zählers.
Das Argument von \displaystyle i/(1+i) ist daher
| \displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.} |
Die Argumente von \displaystyle i und \displaystyle 1+i erhalten wir, indem wir die Zahlen in der komplexen Zahlenebene einzeichnen und ein wenig Trigonometrie anwenden.
Daher erhalten wir
| \displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.} |