Aus Online Mathematik Brückenkurs 2

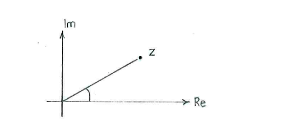
Polar form is an alternative way to express complex numbers. The idea is that it is sufficient to know a complex number's distance from the origin (magnitude) and the angle which the line between the number and the origin makes with the positive real axis (argument), in order to determine the number.

Instead of working with the number's rectangular form, \displaystyle x+iy, we use its magnitude and argument to obtain a simpler and more natural description of e.g. multiplication and division.

The relation between a complex number in rectangular form and in polar form can be written as

\displaystyle x+iy=r(\cos\alpha + i\sin\alpha)\,,

where \displaystyle x and \displaystyle y are the number's real and imaginary parts respectively, and where \displaystyle r and \displaystyle \alpha are the magnitude and the argument, respectively. It is the right-hand side in this formula which is usually said to be the number's polar form.

The number \displaystyle \text{3} has magnitude \displaystyle \text{3} (distance to the origin), and argument \displaystyle 0 because the number lies on the positive real axis. The number's polar form is therefore

\displaystyle 3(\cos 0 + i\sin 0)\,\textrm{.}