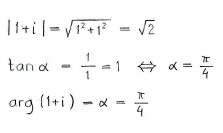Lösung 3.3:1a
Aus Online Mathematik Brückenkurs 2
Powers are repeated multiplications and because multiplication is a relatively simple arithmetical operation when it is carried out in polar form, calculating powers also becomes fairly simple in polar form:
\displaystyle \left( r\left( \cos \alpha +i\sin \alpha \right) \right)^{n}=r^{n}\left( \cos n\alpha +i\sin n\alpha \right)
The equation above is called de Moivre's formula.
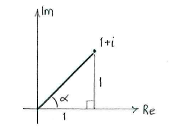
The plan is therefore to rewrite \displaystyle \text{1}+i in polar form, raised the expression to the power \displaystyle \text{12} using de Moivre's formula and then to write the answer in the form \displaystyle a+ib.
Using the calculations above, we see that
\displaystyle \text{1}+i=\sqrt{2}\left( \cos \frac{\pi }{4}+i\sin \frac{\pi }{4} \right)
de Moivre's formula now gives
\displaystyle \begin{align}
& \left( \text{1}+i \right)^{12}=\left( \sqrt{2} \right)^{12}\left( \cos 12\centerdot \frac{\pi }{4}+i\sin 12\centerdot \frac{\pi }{4} \right) \\
& =2^{\frac{1}{2}\centerdot 12}\left( \cos 3\pi +i\sin 3\pi \right) \\
& =2^{6}\left( -1+i\centerdot 0 \right)=64\centerdot \left( -1 \right)=-64 \\
& \\
\end{align}