Aus Online Mathematik Brückenkurs 2

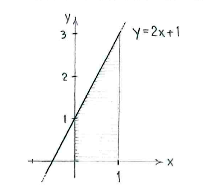
The graph of the function \displaystyle y=2x+1 is a straight line which cuts the y-axis at \displaystyle y=1 and has slope 2.

The integral's value is the area under the straight line and between \displaystyle x=0 and \displaystyle x=1.

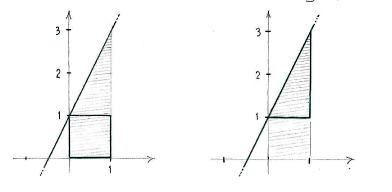
We can divide up the region under the graph into a square and rectangle,

and then add up the area to obtain the total area.

The value of the integral is

\displaystyle \begin{align} \int\limits_{0}^{1} (2x+1)\,dx &= \text{(area of the square)} + \text{(area of the triangle)}\\ &= 1\cdot 1 + \frac{1}{2}\cdot 1\cdot 2 = 2\,\textrm{.} \end{align}