Lösung 2.1:1d
Aus Online Mathematik Brückenkurs 2
The modulus function, \displaystyle \left| x \right|, strips \displaystyle x of its sign, e.g.
\displaystyle \left| -5 \right|=5,
\displaystyle \left| 3 \right|=3
and
\displaystyle \left| -\pi \right|=\pi
For positive values of
\displaystyle x, the modulus function has no effect, since
\displaystyle \left| x \right|=x, but for negative
\displaystyle x
the modulus function changes the sign of
\displaystyle x, i.e.
\displaystyle \left| -x \right|=x
(remember that
\displaystyle x
is negative and therefore
\displaystyle -x
is positive).
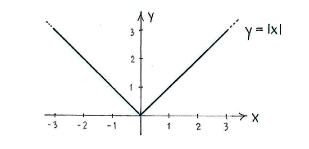
If we draw a graph of \displaystyle y=\left| x \right| it will consist of two parts. For \displaystyle x\ge 0 we have \displaystyle y=x, and for \displaystyle x\le 0 we have \displaystyle y=-x
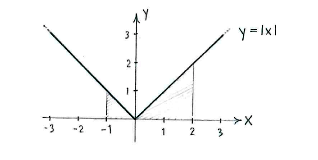
The value of the integral is the area of the region under the graph
\displaystyle y=\left| x \right|
and between
\displaystyle x=-1
and
\displaystyle x=2.
This region consists of two triangles and we therefore obtain
\displaystyle \int\limits_{-1}^{2}{\left| x \right|}\,dx=\frac{1}{2}\centerdot 1\centerdot 1+\frac{1}{2}\centerdot 2\centerdot 2=\frac{5}{2}