Aus Online Mathematik Brückenkurs 2

The whole procedure can be illustrated by the figure below:

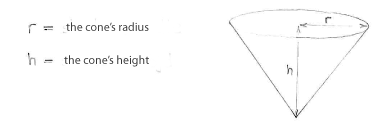
Because it is the cornet's volume we want to maximise, it is appropriate to start by introducing some notation for the dimensions of the cornet.

\displaystyle r=\text{ } the cone's radius \displaystyle h=\text{ } the cone's height

With these dimensions, the volume of the cornet will be the same as that of a cone:

\displaystyle \begin{align} & V=\frac{1}{3}\text{(area of upper circle)}\bullet \text{(height)} \\ & =\frac{1}{3}\pi r^{2}h \\ \end{align}

To go further, we now need to express the radius \displaystyle r and the height \displaystyle h in terms of the angle \displaystyle \alpha on the removed circular sector, so that we can the maximum of the volume \displaystyle V when \displaystyle \alpha varies.

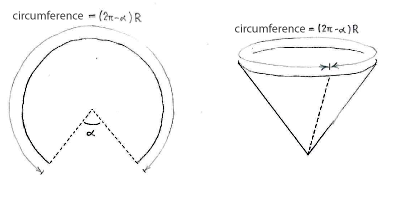
When we cut out a circular sector of angle \displaystyle \alpha from a circular disk, the remaining part of the circular disc's periphery will have length \displaystyle \left( 2\pi -\alpha \right)R, where \displaystyle R is the radius of the circular disc. This periphery will then become the cornet's upper circular edge, which therefore has the same circumference.

On the other hand, the cornet's upper circular edge has a circumference \displaystyle 2\pi r, so we must therefore have the relation

\displaystyle 2\pi r=\left( 2\pi -\alpha \right)R\quad \Leftrightarrow \quad r=\frac{2\pi -\alpha }{2\pi }R

We have thus managed to express the radius \displaystyle r in terms of the angle \displaystyle \alpha (and the radius \displaystyle R of the original circle).

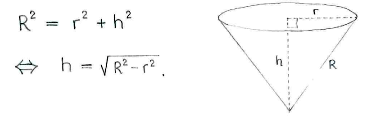
In order to obtain the height \displaystyle h, we can use the fact that we know that the distance from the cornet's tip to its upper edge is equal to the radius \displaystyle R of the original circle. Pythagoras' theorem now gives:

\displaystyle \begin{align} & R^{2}=r^{2}+h^{2} \\ & \Leftrightarrow \quad h=\sqrt{R^{2}-r^{2}} \\ \end{align}

This means that

\displaystyle \begin{align} & h=\sqrt{R^{2}-\left( \frac{2\pi -\alpha }{2\pi }R \right)^{2}}=\sqrt{R^{2}-\left( \frac{2\pi -\alpha }{2\pi } \right)^{2}R^{2}} \\ & =R\sqrt{1-\left( \frac{2\pi -\alpha }{2\pi } \right)^{2}} \\ \end{align}

Hence, we have expressed \displaystyle r and \displaystyle h in terms of the angle \displaystyle \alpha and the radius \displaystyle R, and we get that the volume of the cornet is given by

\displaystyle \begin{align} & V=\frac{1}{3}\pi r^{2}h=\frac{1}{3}\pi \left( \frac{2\pi -\alpha }{2\pi }R \right)^{2}R\sqrt{1-\left( \frac{2\pi -\alpha }{2\pi } \right)^{2}} \\ & =\frac{1}{3}\pi R^{3}\left( \frac{2\pi -\alpha }{2\pi } \right)^{2}\sqrt{1-\left( \frac{2\pi -\alpha }{2\pi } \right)^{2}} \\ \end{align}

At last, we can mathematically formulate the problem:

Maximise \displaystyle V\left( \alpha \right)=\frac{1}{3}\pi R^{3}\left( \frac{2\pi -\alpha }{2\pi } \right)^{2}\sqrt{1-\left( \frac{2\pi -\alpha }{2\pi } \right)^{2}} where \displaystyle 0\le \alpha \le 2\pi

Before we start to try and solve this problem, we can observe that the variable \displaystyle \alpha occurs in the volume function only in the combination \displaystyle \frac{2\pi -\alpha }{2\pi }, so that we may as well choose to maximise the volume with respect to the variable \displaystyle x=\frac{2\pi -\alpha }{2\pi } to obtain, as far as the formula is concerned, the somewhat easier problem:

Maximise \displaystyle V\left( x \right)=\frac{1}{3}\pi R^{3}x^{2}\sqrt{1-x^{2}} when \displaystyle 0\le x\le 1.

When either \displaystyle x=0\text{ } or \displaystyle x=1, the volume is zero and since the volume function is a differentiable function of \displaystyle x (apart from at \displaystyle x=1 ), the volume must be a maximum at a critical point of the function.

We differentiate

\displaystyle \begin{align} & {V}'\left( x \right)=\frac{1}{3}\pi R^{3}\bullet 2x\bullet \sqrt{1-x^{2}}+\frac{1}{3}\pi R^{3}x^{3}\bullet \frac{1}{2\sqrt{1-x^{2}}}\bullet \left( -2x \right) \\ & \\ \end{align}

and begin simplifying this expression. The strategy is to try to take out as many factors as possible, so that we see more easily when some factor, and hence the derivative, becomes zero:

\displaystyle \begin{align} & {V}'\left( x \right)=\frac{2}{3}\pi R^{3}x\sqrt{1-x^{2}}-\frac{1}{3}\pi R^{3}x^{3}\frac{1}{\sqrt{1-x^{2}}} \\ & =\frac{1}{3}\pi R^{3}\frac{x}{\sqrt{1-x^{2}}}\left[ 2\left( 1-x^{2} \right)-x^{2} \right] \\ & =\frac{1}{3}\pi R^{3}\frac{x}{\sqrt{1-x^{2}}}\left( 2-3x^{2} \right) \\ \end{align}

The derivative is zero when \displaystyle x=0 (which is an endpoint) or when \displaystyle 2-3x^{2}=0, i.e. \displaystyle x=\sqrt{{2}/{3}\;} ( \displaystyle x=-\sqrt{{2}/{3}\;} lies outside \displaystyle 0\le x\le 1 ).

With the help of a table of the sign of the factors' derivative's

TABLE

we can write down a table of the sign of the derivative itself,

TABLE

and see that \displaystyle x=\sqrt{{2}/{3}\;} is a global maximum. The value \displaystyle x=\sqrt{{2}/{3}\;} corresponds to the \displaystyle \alpha -value

\displaystyle \sqrt{\frac{2}{3}}=\frac{2\pi -\alpha }{2\pi }\quad \Leftrightarrow \quad \alpha =2\pi \left( 1-\sqrt{{2}/{3}\;} \right) radians