Lösung 3.2:1b
Aus Online Mathematik Brückenkurs 2
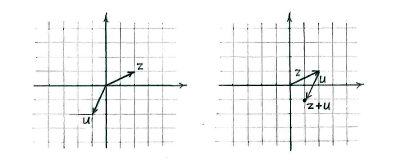
We can easily calculate \displaystyle z+u and \displaystyle z-u,
\displaystyle \begin{align}z+u&=2+i+(-1-2i)=2-1+(1-2)i=1-i,\\ z-u&=2+i-(-1-2i)=2+1+(1+2)i=3+3i,\end{align}
and then mark them on the complex plane.
An alternative is to view \displaystyle z and \displaystyle u as vectors and \displaystyle z+u as a vector addition of \displaystyle z and \displaystyle u.
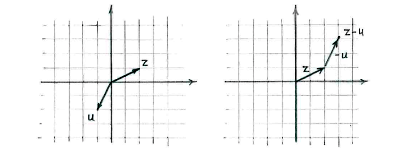
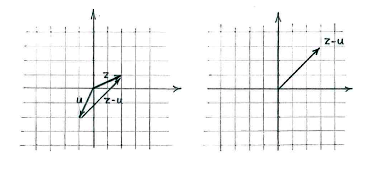
We can either view the vector subtraction \displaystyle z-u as \displaystyle z+(-u),
or interpret \displaystyle z-u from the vector relation
\displaystyle z=(z-u)+u
i.e. \displaystyle z-u is the vector we add to \displaystyle u to arrive at \displaystyle z.