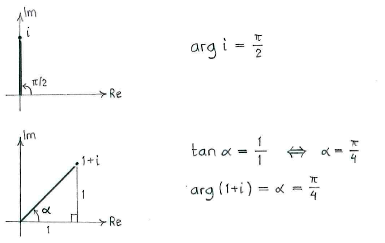Lösung 3.2:5d
Aus Online Mathematik Brückenkurs 2
When dividing two complex numbers, the numerator's magnitude is divided by the denominator's magnitude and the numerator's argument is subtracted from the numerator's argument.
The argument of the quotient \displaystyle i/(1+i) is therefore
| \displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i)\,\textrm{.} |
We obtain the argument of \displaystyle i and \displaystyle 1+i by drawing the numbers in the complex plane and using a little trigonometry.
Hence, we obtain
| \displaystyle \arg\frac{i}{1+i} = \arg i - \arg (1+i) = \frac{\pi}{2} - \frac{\pi}{4} = \frac{\pi}{4}\,\textrm{.} |