Aus Online Mathematik Brückenkurs 2

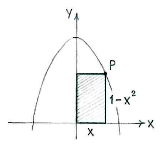
If we call the x-coordinate of the point \displaystyle P \displaystyle x, then its y-coordinate is \displaystyle 1-x^{2}, because \displaystyle P lies on the curve \displaystyle y=1-x^{2}.

The area of the rectangle is then given by

\displaystyle A(x) = \text{(base)}\cdot\text{(height)} = x\cdot (1-x^2)

and we will try to choose \displaystyle x so that this area function is maximised.

To begin with, we note that, because \displaystyle P should lie in the first quadrant, \displaystyle x\ge 0 and also \displaystyle y=1-x^2\ge 0, i.e. \displaystyle x\le 1. We should therefore look for the maximum of \displaystyle A(x) when \displaystyle 0\le x\le 1\,.

There are three types of points which can maximise the area function:

1. critical points,
2. points where the function is not differentiable,
3. endpoints of the region of definition.

The function \displaystyle A(x) = x(1-x^2) is differentiable everywhere, so item 2 does not apply. In addition, \displaystyle A(0) = A(1) = 0\,, so the endpoints in item 3 cannot be maximum points (but rather the opposite, i.e. minimum points).

We must therefore conclude that the maximum area is a critical point. We differentiate

\displaystyle A'(x) = 1\cdot (1-x^2) + x\cdot (-2x) = 1-3x^2\,,

and the condition that the derivative should be zero gives that \displaystyle x=\pm 1/\!\sqrt{3}; however, it is only \displaystyle x=1/\!\sqrt{3} which satisfies \displaystyle 0\le x\le 1.

At the critical point, the second derivative \displaystyle A''(x)=-6x has the value

\displaystyle A''\bigl( 1/\!\sqrt{3}\bigr) = -6\cdot\frac{1}{\sqrt{3}} < 0\,,

which shows that \displaystyle x=1/\!\sqrt{3} is a local maximum.

The answer is that the point \displaystyle P should be chosen so that

\displaystyle P = \Bigl(\frac{1}{\sqrt{3}}, 1-\Bigl(\frac{1}{\sqrt{3}} \Bigr)^2\, \Bigr) = \Bigl(\frac{1}{\sqrt{3}}, \frac{2}{3} \Bigr)\,\textrm{.}