Aus Online Mathematik Brückenkurs 2

In order to determine the function's extreme points, we investigate three types of points,

1. critical points, i.e. where \displaystyle f^{\,\prime}(x)=0,
2. points where the function is not differentiable, and
3. endpoints of the interval of definition.

In our case, we have that:

1. The derivative of \displaystyle f(x) is given by

   \displaystyle f^{\,\prime}(x) = 3-2x

   and becomes zero when \displaystyle x=3/2\,.
2. The function is a polynomial, and is therefore differentiable everywhere.
3. The function is defined for all x, and therefore the interval of definition has no endpoints.

There is thus just one point \displaystyle x=3/2\,, where the function possibly has an extreme point.

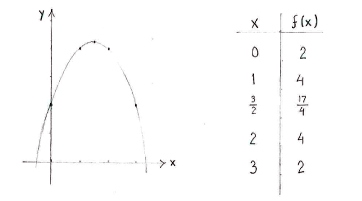
If we write down a sign table for the derivative, we see that \displaystyle x=3/2 is a local maximum.

\displaystyle x		\displaystyle \tfrac{3}{2}
\displaystyle f^{\,\prime}(x)	\displaystyle +	\displaystyle 0	\displaystyle -
\displaystyle f(x)	\displaystyle \nearrow	\displaystyle \tfrac{17}{4}	\displaystyle \searrow

Because the function is given by a second-degree expression, its graph is a parabola with a maximum at \displaystyle (3/2, 17/4) and we can draw it with the help of a few couple of points.