Lösung 3.2:2e

Because the expression contains both \displaystyle z and \displaystyle \bar{z}, we write out \displaystyle z=x+iy, where \displaystyle x is the real part of \displaystyle z and \displaystyle y is the imaginary part. Thus, we have

\displaystyle \mathrm{Re}z=x

\displaystyle i+\bar{z}=i+(x-iy)=x+(1-y)i

and the condition becomes

\displaystyle x=x+(1-y)i \iff 0=(1-y)i

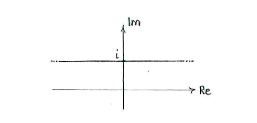
which means that \displaystyle y=1.

The set therefore consists of all complex numbers with imaginary part \displaystyle 1.