Aus Online Mathematik Brückenkurs 2

The integral is a standard integral, with \displaystyle \text{5}x as the argument of the cosine function. If we therefore substitute \displaystyle u=\text{5}x, we obtain the “correct” argument of the cosine,

\displaystyle \begin{align} & \int\limits_{0}^{\pi }{\cos 5x\,dx=\left\{ \begin{array}{*{35}l} u=\text{5}x \\ du=\left( 5x \right)^{\prime }\,dx=5\,dx \\ \end{array} \right\}} \\ & =\frac{1}{5}\int\limits_{0}^{5\pi }{\cos u\,du} \\ \end{align}

As can be seen, the variable change replaced \displaystyle dx by \displaystyle \frac{1}{5}\,du and the new limits of integration become \displaystyle u=5\centerdot 0=0 and \displaystyle u=5\centerdot \pi =5\pi .

Now, we have a standard integral which can easily compute:

\displaystyle \begin{align} & \frac{1}{5}\int\limits_{0}^{5\pi }{\cos u\,du}=\frac{1}{5}\left[ \sin u \right]_{0}^{5\pi } \\ & =\frac{1}{5}\left( \sin 5\pi -\sin 0 \right)=\frac{1}{5}\left( 0-0 \right)=0 \\ \end{align}

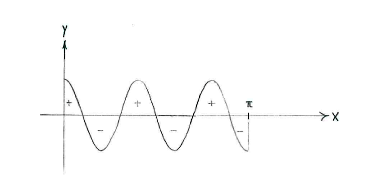
NOTE: if we draw the graph for \displaystyle y=\cos 5x, we see also that the area between the curve and \displaystyle x -axis above the \displaystyle x -axis is the same as the area under the \displaystyle x -axis.