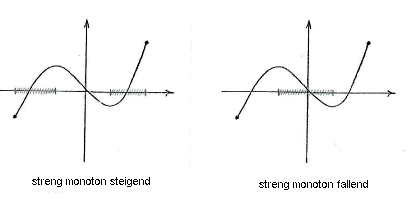Aus Online Mathematik Brückenkurs 2

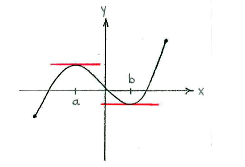
Es gibt zwei Punkte, \displaystyle x=a und \displaystyle x=b (siehe Bild), bei denen die Ableitung null ist. Dies sind die stationären Punkte.

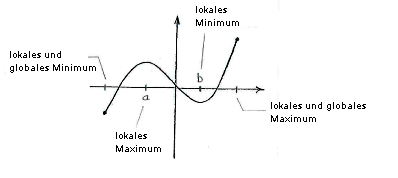
Weiter hat die Funktion im linken Endpunkt und im Punkt \displaystyle x=b ein lokales Minimum. Die Funktion hat lokale Maxima im Punkt \displaystyle x=a und im rechten Endpunkt.

Von diesen Punkten ist der linke Endpunkt das globale Minimum und der Punkt \displaystyle x=a das globale Maximum.

Die Funktion ist zwischen dem linken Endpunkt und \displaystyle x=a streng monoton steigend sowie zwischen \displaystyle x=b und dem rechten Endpunkt. Zwischen \displaystyle x=0 und \displaystyle x=b ist die Funktion streng monoton fallend.