Lösung 3.2:2d
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
| Zeile 1: | Zeile 1: | ||
| - | Allgemein bedeutet <math>|z-w|</math> der Abstand zwischen den komplexen Zahlen <math>z</math> und <math>w</math>. Schreiben wir die Gleichung also | + | Allgemein bedeutet <math>|z-w|</math> der Abstand zwischen den komplexen Zahlen <math>z</math> und <math>w</math>. Schreiben wir die Gleichung also als |
{{Abgesetzte Formel||<math>|z-(1+i)|=3</math>}} | {{Abgesetzte Formel||<math>|z-(1+i)|=3</math>}} | ||
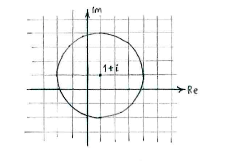
| - | sehen wir dass der Abstand zwischen <math>z</math> und <math>1+i</math> 3 sein soll, | + | sehen wir, dass der Abstand zwischen <math>z</math> und <math>1+i</math> 3 sein soll, also ist unsere Fläche ein Kreis mit dem Radius 3 und dem Mittelpunkt <math>1+i</math>. |
[[Image:3_2_2_d.gif|center]] | [[Image:3_2_2_d.gif|center]] | ||
Version vom 16:02, 22. Aug. 2009
Allgemein bedeutet \displaystyle |z-w| der Abstand zwischen den komplexen Zahlen \displaystyle z und \displaystyle w. Schreiben wir die Gleichung also als
| \displaystyle |z-(1+i)|=3 |
sehen wir, dass der Abstand zwischen \displaystyle z und \displaystyle 1+i 3 sein soll, also ist unsere Fläche ein Kreis mit dem Radius 3 und dem Mittelpunkt \displaystyle 1+i.