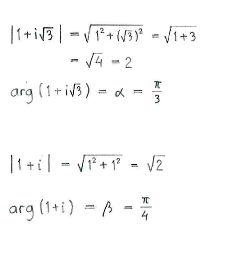Lösung 3.2:6e
Aus Online Mathematik Brückenkurs 2
K (Solution 3.2:6e moved to Lösung 3.2:6e: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| + | Können wir den Zähler und den Nenner auf Polarform bringen, können wir die Division einfach ausführen, indem wir | ||
If we manage to write the numerator and denominator in polar form, we can then use the fact that when division is carried out in polar form it is particularly simple. Division means, namely, that the numerator's magnitude is divided by the denominator's magnitude and that the numerator's argument is subtracted from denominator's argument or, in written form, | If we manage to write the numerator and denominator in polar form, we can then use the fact that when division is carried out in polar form it is particularly simple. Division means, namely, that the numerator's magnitude is divided by the denominator's magnitude and that the numerator's argument is subtracted from denominator's argument or, in written form, | ||
Version vom 13:13, 13. Mai 2009
Können wir den Zähler und den Nenner auf Polarform bringen, können wir die Division einfach ausführen, indem wir If we manage to write the numerator and denominator in polar form, we can then use the fact that when division is carried out in polar form it is particularly simple. Division means, namely, that the numerator's magnitude is divided by the denominator's magnitude and that the numerator's argument is subtracted from denominator's argument or, in written form,
| \displaystyle \frac{r_1(\cos\alpha+i\sin\alpha)}{r_2(\cos\beta+i\sin\beta)} = \frac{r_1}{r_2}\bigl(\cos (\alpha-\beta) + i\sin (\alpha-\beta)\bigr)\,\textrm{.} |
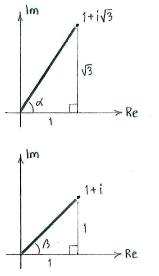
Thus, we determine the numerator's and denominator's polar forms:
Now, we obtain
| \displaystyle \begin{align}
\frac{1+i\sqrt{3}}{1+i} &= \frac{2\Bigl(\cos\dfrac{\pi}{3}+i\sin\dfrac{\pi}{3}\Bigr)}{\sqrt{2}\Bigl(\cos \dfrac{\pi}{4} + i\sin\dfrac{\pi}{4}\Bigr)}\\[5pt] &= \frac{2}{\sqrt{2}}\Bigl( \cos\Bigl(\frac{\pi}{3}-\frac{\pi}{4}\Bigr) + i\sin\Bigl( \frac{\pi}{3}-\frac{\pi}{4}\Bigr)\Bigr)\\[5pt] &= \sqrt{2}\Bigl(\cos\frac{\pi}{12}+i\sin\frac{\pi}{12}\Bigr)\,\textrm{.} \end{align} |