Aus Online Mathematik Brückenkurs 2

Version vom 10:13, 11. Mär. 2009 (bearbeiten) Tekbot (Diskussion | Beiträge) K (Solution 1.3:6 moved to Lösung 1.3:6: Robot: moved page) ← Zum vorherigen Versionsunterschied		Version vom 12:19, 27. Apr. 2009 (bearbeiten) (rückgängig) Martin (Diskussion | Beiträge) Zum nächsten Versionsunterschied →
Zeile 1:		Zeile 1:
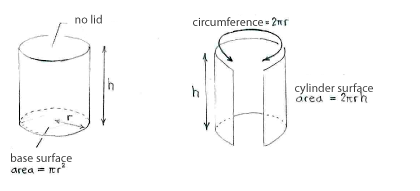
-	If we call the radius of the metal can ''r'' and its height ''h'', then we can determine the can's volume and area by using the figures below,	+	Wir benennen den Radius der Tasse ''r'' und die Höhe ''h''. Der Volumen ist
	{{Abgesetzte Formel||<math>\begin{align}		{{Abgesetzte Formel||<math>\begin{align}
-	\text{Volume} &= \text{(area of the base)}\cdot\text{(height)}\\[5pt]	+	\text{Volume} &= \text{(Fläche der Basis)}\cdot\text{(Höhe)}\\[5pt]
	&= \pi r^2\cdot h\,,\\[10pt]		&= \pi r^2\cdot h\,,\\[10pt]
-	\text{Area} &= \text{(area of the base)} + \text{(area of the cylindrical surface)}\\[5pt]	+	\text{Fläche} &= \text{(Fläche der Basis)} + \text{(Fläche des Zylinders)}\\[5pt]
	&= \pi r^2 + 2\pi rh\,\textrm{.}		&= \pi r^2 + 2\pi rh\,\textrm{.}
	\end{align}</math>}}		\end{align}</math>}}
Zeile 10:		Zeile 10:
	[[Image:1_3_6_1.gif|center]]		[[Image:1_3_6_1.gif|center]]
-	The problem can then be formulated as: minimise the can's area, <math>A = \pi r^2 + 2\pi h</math>, whilst at the same time keeping the volume, <math>V = \pi r^2h\,</math>, constant.	+	Das Problem ist also; Minimiere die Fläche <math>A = \pi r^2 + 2\pi h</math>, während der Volumen <math>V = \pi r^2h\,</math>, konstant ist.
-	From the formula for the volume, we can make ''h'' the subject,	+	Wir schreiben ''h'' als Funktion des Volumen,
	{{Abgesetzte Formel||<math>h=\frac{V}{\pi r^2}</math>}}		{{Abgesetzte Formel||<math>h=\frac{V}{\pi r^2}</math>}}
-	and express the area solely in terms of the radius, ''r'',	+	und können dadurch die Fläche als Funktion von ''r'' schreiben,
	{{Abgesetzte Formel||<math>A = \pi r^2 + 2\pi r\cdot\frac{V}{\pi r^2} = \pi r^2 + \frac{2V}{r}\,\textrm{.}</math>}}		{{Abgesetzte Formel||<math>A = \pi r^2 + 2\pi r\cdot\frac{V}{\pi r^2} = \pi r^2 + \frac{2V}{r}\,\textrm{.}</math>}}
-	The minimisation problem is then:	+	Unser Problem ist dann
-	::Minimise the area <math>A(r) = \pi r^2 + \frac{2V}{r}</math>, when <math>r>0\,</math>.	+	::Minimiere die Flächea <math>A(r) = \pi r^2 + \frac{2V}{r}</math>, wenn <math>r>0\,</math>.
-	The area function <math>A(r)</math> is differentiable for all <math>r>0</math> and the region of definition <math>r>0</math> has no endpoints (<math>r=0</math> does not satisfy <math>r>0</math>), so the function can only assume extreme values at critical points.	+	Die Funktion <math>A(r)</math> ist für alle <math>r>0</math> differenzierbar, und der Bereich <math>r>0</math> hat keine Endpunkte (nachdem <math>r=0</math> nicht <math>r>0</math> erfüllt), und also erscheinen Extrempunkte nur in stationären Punkten.
-	The derivative is given by	+	Die Ableitung ist
	{{Abgesetzte Formel||<math>A'(r) = 2\pi r - \frac{2V}{r^2}\,,</math>}}		{{Abgesetzte Formel||<math>A'(r) = 2\pi r - \frac{2V}{r^2}\,,</math>}}
-	and if we set the derivative equal to zero, so as to obtain the critical points, we get	+	Und die Ableitung gleich null ergibt folgende Gleichung
	{{Abgesetzte Formel||<math>\begin{align}		{{Abgesetzte Formel||<math>\begin{align}
Zeile 37:		Zeile 37:
	\end{align}</math>}}		\end{align}</math>}}
-	For this value of ''r'', the second derivative,	+	Die zweite Ableitung ist
	{{Abgesetzte Formel||<math>A''(r) = 2\pi + \frac{4V}{r^3}\,,</math>}}		{{Abgesetzte Formel||<math>A''(r) = 2\pi + \frac{4V}{r^3}\,,</math>}}
-	has the value	+	und hat den Wert
	{{Abgesetzte Formel||<math>A''\bigl(\sqrt[3]{V/\pi}\bigr) = 2\pi + \frac{4V}{V/\pi } = 6\pi > 0\,,</math>}}		{{Abgesetzte Formel||<math>A''\bigl(\sqrt[3]{V/\pi}\bigr) = 2\pi + \frac{4V}{V/\pi } = 6\pi > 0\,,</math>}}
-	which shows that <math>r=\sqrt[3]{V/\pi}</math> is a local minimum.	+	im stationären Punkt.
-	Because the region of definition, <math>r>0</math>, is open (the endpoint	+	Also ist <math>r=\sqrt[3]{V/\pi}</math> ein lokales Minima.
-	<math>r=0\text{ }</math> is not included) and unlimited, we cannot directly say that the area is least when <math>r = \sqrt[3]{V/\pi}\,</math>; it could be the case that area becomes smaller when <math>r\to 0</math> or <math>r\to \infty </math>. In this case, however, the area increases without bound as	+
-	<math>r\to 0</math> or <math>r\to \infty </math>, so <math>r=\sqrt[3]{V/\pi}</math>	+
-	really is a global minimum.	+
-	The metal can has the least area for a given volume <math>V</math> when	+	Nachdem wir kein begrenztes Intervall haben, können wir nicht direkt ausschließen dass die Fläche kleiner wird wenn <math>r\to 0</math> oder wenn <math>r\to \infty </math>. In unseren Fall wächst die Fläche aber unbegrenzt in den beiden Richtungen <math>r\to 0</math> und <math>r\to \infty </math>, und also ist
		+	<math>r=\sqrt[3]{V/\pi}</math> ein globales Minima.
		+
		+	Also ist die Fläche minimal wenn
	{{Abgesetzte Formel||<math>\begin{align}		{{Abgesetzte Formel||<math>\begin{align}

---

Version vom 12:19, 27. Apr. 2009

Wir benennen den Radius der Tasse r und die Höhe h. Der Volumen ist

\displaystyle \begin{align} \text{Volume} &= \text{(Fläche der Basis)}\cdot\text{(Höhe)}\\[5pt] &= \pi r^2\cdot h\,,\\[10pt] \text{Fläche} &= \text{(Fläche der Basis)} + \text{(Fläche des Zylinders)}\\[5pt] &= \pi r^2 + 2\pi rh\,\textrm{.} \end{align}

Das Problem ist also; Minimiere die Fläche \displaystyle A = \pi r^2 + 2\pi h, während der Volumen \displaystyle V = \pi r^2h\,, konstant ist.

Wir schreiben h als Funktion des Volumen,

\displaystyle h=\frac{V}{\pi r^2}

und können dadurch die Fläche als Funktion von r schreiben,

\displaystyle A = \pi r^2 + 2\pi r\cdot\frac{V}{\pi r^2} = \pi r^2 + \frac{2V}{r}\,\textrm{.}

Unser Problem ist dann

Minimiere die Flächea \displaystyle A(r) = \pi r^2 + \frac{2V}{r}, wenn \displaystyle r>0\,.

Die Funktion \displaystyle A(r) ist für alle \displaystyle r>0 differenzierbar, und der Bereich \displaystyle r>0 hat keine Endpunkte (nachdem \displaystyle r=0 nicht \displaystyle r>0 erfüllt), und also erscheinen Extrempunkte nur in stationären Punkten.

Die Ableitung ist

\displaystyle A'(r) = 2\pi r - \frac{2V}{r^2}\,,

Und die Ableitung gleich null ergibt folgende Gleichung

\displaystyle \begin{align} & 2\pi r - \frac{2V}{r^2} = 0\quad \Leftrightarrow \quad 2\pi r = \frac{2V}{r^2}\\[5pt] &\quad\Leftrightarrow \quad r^3=\frac{V}{\pi}\quad \Leftrightarrow \quad r=\sqrt[\scriptstyle 3]{\frac{V}{\pi}}\,\textrm{.} \end{align}

Die zweite Ableitung ist

\displaystyle A''(r) = 2\pi + \frac{4V}{r^3}\,,

und hat den Wert

\displaystyle A''\bigl(\sqrt[3]{V/\pi}\bigr) = 2\pi + \frac{4V}{V/\pi } = 6\pi > 0\,,

im stationären Punkt.

Also ist \displaystyle r=\sqrt[3]{V/\pi} ein lokales Minima.

Nachdem wir kein begrenztes Intervall haben, können wir nicht direkt ausschließen dass die Fläche kleiner wird wenn \displaystyle r\to 0 oder wenn \displaystyle r\to \infty . In unseren Fall wächst die Fläche aber unbegrenzt in den beiden Richtungen \displaystyle r\to 0 und \displaystyle r\to \infty , und also ist

\displaystyle r=\sqrt[3]{V/\pi} ein globales Minima.

Also ist die Fläche minimal wenn

\displaystyle \begin{align} r &= \sqrt[3]{V/\pi}\,,\quad\text{and}\\[5pt] h &= \frac{V}{\pi r^{2}} = \frac{V}{\pi}\Bigl(\frac{V}{\pi}\Bigr)^{-2/3} = \Bigl( \frac{V}{\pi}\Bigr)^{1-2/3} = \Bigl(\frac{V}{\pi}\Bigr)^{1/3} = \sqrt[3]{\frac{V}{\pi}}\,\textrm{.} \end{align}