Lösung 1.3:2c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 1.3:2c moved to Lösung 1.3:2c: Robot: moved page)
Zeile 1: Zeile 1:
-
There are three types of points at which the function can have local extreme points,
+
Lokale Extrempunkte einer Funktion sind entweder:
-
# critical points, i.e. where <math>f^{\,\prime}(x)=0</math>,
+
# stationäre Punkte, wo <math>f^{\,\prime}(x)=0</math>,
-
# points where the function is not differentiable, and
+
# Singuläre Punkte, wo die Funktion nicht ableitbar ist, oder
-
# endpoints of the interval of definition.
+
# Endpunkte.
 +
 +
Nachdem die Funktion ein Polynom ist, ist sie überall definiert, und überall ableitbar. Also gibt es keine Extrempunkte die die Bedienungen 2 und 3 erfüllen.
-
Because our function is a polynomial, it is defined and differentiable everywhere, and therefore does not have any points which satisfy items 2 and 3.
+
Die Ableitung als null gesetzt ergibt folgende Gleichung
-
 
+
-
As regards item 1, we set the derivative equal to zero and obtain the equation
+
{{Abgesetzte Formel||<math>f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}</math>}}
-
Dividing both sides by 6 and completing the square, we obtain
+
Dividieren wir durch 6 erhalten wir durch quadratische Ergänzung
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}</math>}}
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}</math>}}
-
This gives us the equation
+
Und wir erhalten die Gleichung
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}</math>}}
{{Abgesetzte Formel||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}</math>}}
-
and taking the square root gives the solutions
+
mit den Lösungen
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 29: Zeile 29:
<math>x=-2</math> and <math>x=1</math>.
<math>x=-2</math> and <math>x=1</math>.
-
Then, we write down a sign table for the derivative, and read off the possible extreme points.
+
Wir erstellen eine Vorzeichentabelle, und erhalten so die Extrempunkte.
{| border="1" cellpadding="5" cellspacing="0" align="center"
{| border="1" cellpadding="5" cellspacing="0" align="center"
Zeile 55: Zeile 55:
|}
|}
 +
Die Funktion hat also ein lokales Maxima in <math>x=-2</math> und ein lokales Minima in <math>x=1</math>.
-
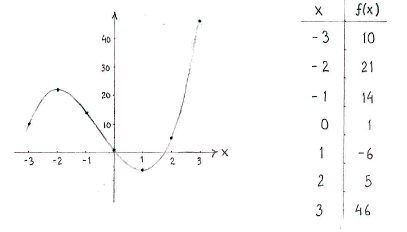
The function has a local maximum at <math>x=-2</math> and a local minimum at <math>x=1</math>.
+
Berechnen wir den Funktionswert in einigen Punkten, können wir mit Hilfe der Vorzeichentabelle die Funktion zeichnen.
-
 
+
-
We obtain the overall appearance of the graph of the function from the table and by calculating the value of the function at a few points.
+
[[Image:1_3_2_c.gif|center]]
[[Image:1_3_2_c.gif|center]]

Version vom 16:30, 26. Apr. 2009

Lokale Extrempunkte einer Funktion sind entweder:

  1. stationäre Punkte, wo \displaystyle f^{\,\prime}(x)=0,
  2. Singuläre Punkte, wo die Funktion nicht ableitbar ist, oder
  3. Endpunkte.

Nachdem die Funktion ein Polynom ist, ist sie überall definiert, und überall ableitbar. Also gibt es keine Extrempunkte die die Bedienungen 2 und 3 erfüllen.

Die Ableitung als null gesetzt ergibt folgende Gleichung

\displaystyle f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}

Dividieren wir durch 6 erhalten wir durch quadratische Ergänzung

\displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}

Und wir erhalten die Gleichung

\displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}

mit den Lösungen

\displaystyle \begin{align}

x &= -\frac{1}{2}-\sqrt{\frac{9}{4}} = -\frac{1}{2}-\frac{3}{2} = -2\,,\\[5pt] x &= -\frac{1}{2}+\sqrt{\frac{9}{4}} = -\frac{1}{2}+\frac{3}{2} = 1\,\textrm{.} \end{align}

This means that if the function has several extreme points, they must be among \displaystyle x=-2 and \displaystyle x=1.

Wir erstellen eine Vorzeichentabelle, und erhalten so die Extrempunkte.

\displaystyle x \displaystyle -2 \displaystyle 1
\displaystyle f^{\,\prime}(x) \displaystyle + \displaystyle 0 \displaystyle - \displaystyle 0 \displaystyle +
\displaystyle f(x) \displaystyle \nearrow \displaystyle 21 \displaystyle \searrow \displaystyle -6 \displaystyle \nearrow

Die Funktion hat also ein lokales Maxima in \displaystyle x=-2 und ein lokales Minima in \displaystyle x=1.

Berechnen wir den Funktionswert in einigen Punkten, können wir mit Hilfe der Vorzeichentabelle die Funktion zeichnen.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:2c“