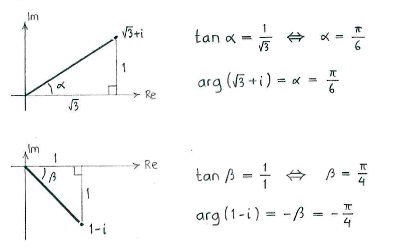Lösung 3.2:5c
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (Solution 3.2:5c moved to Lösung 3.2:5c: Robot: moved page) |
Version vom 10:39, 11. Mär. 2009
Geometrically, the multiplication of two complex numbers means that there magnitudes are multiplied and their arguments are added. The product \displaystyle (\sqrt{3}+i)(1-i) therefore has an argument which is the sum of the argument for the \displaystyle \sqrt{3}+i and \displaystyle 1-i, i.e.
| \displaystyle \arg \bigl((\sqrt{3}+i)(1-i)\bigr) = \arg (\sqrt{3}+i) + \arg (1-i)\,\textrm{.} |
By drawing the factors in the complex plane, we can determine relatively easily the argument using simple trigonometry.
(Because \displaystyle 1-i lies in the fourth quadrant, the argument equals \displaystyle -\beta and not \displaystyle \beta.)
Hence,
| \displaystyle \arg \bigl((\sqrt{3}+i)(1-i)\bigr) = \arg (\sqrt{3}+i) + \arg (1-i) = \frac{\pi}{6} - \frac{\pi}{4} = -\frac{\pi}{12}\,\textrm{.} |
Note: If you prefer to give the argument between \displaystyle 0 and \displaystyle 2\pi , then the answer is
| \displaystyle -\frac{\pi}{12}+2\pi = \frac{-\pi+24\pi}{12} = \frac{23\pi}{12}\,\textrm{.} |