Lösung 3.2:4a
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (Solution 3.2:4a moved to Lösung 3.2:4a: Robot: moved page) |
Version vom 10:37, 11. Mär. 2009
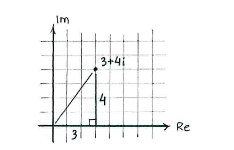
The magnitude of the number \displaystyle 3+4i is the number's distance to the origin in the complex number plane.
If we treat the line from the origin to \displaystyle 3+4i as the hypotenuse in a right-angled triangle which has its legs parallel with the real and imaginary axes, then the Pythagorean theorem gives that the magnitude is
| \displaystyle |3+4i| = \sqrt{3^2+4^2} = \sqrt{9+16} = \sqrt{25} = 5\,\textrm{.} |
Note: In general, the magnitude of a complex number \displaystyle z=x+iy is equal to
| \displaystyle |z| = |x+iy| = \sqrt{x^2+y^2}\,\textrm{.} |