Lösung 3.2:1c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
By calculation, we obtain
By calculation, we obtain
-
{{Displayed math||<math>2z+w = 2(2+i)+(2+3i) = 2\cdot 2 + 2 + (2+3)i = 6+5i</math>}}
+
{{Abgesetzte Formel||<math>2z+w = 2(2+i)+(2+3i) = 2\cdot 2 + 2 + (2+3)i = 6+5i</math>}}
and we can mark this point on the complex plane.
and we can mark this point on the complex plane.

Version vom 13:07, 10. Mär. 2009

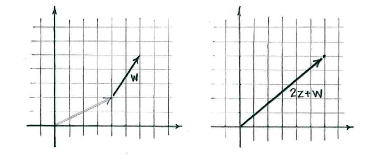
By calculation, we obtain

\displaystyle 2z+w = 2(2+i)+(2+3i) = 2\cdot 2 + 2 + (2+3)i = 6+5i

and we can mark this point on the complex plane.

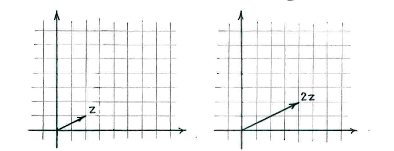
If we treat \displaystyle z and \displaystyle w as vectors, then \displaystyle 2z is the vector which has the same direction as \displaystyle z, but is twice as long.

We add \displaystyle w to this vector and get \displaystyle 2z+w.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:1c“