Lösung 2.1:4b
Aus Online Mathematik Brückenkurs 2
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
By completing the square of the equation of the curve | By completing the square of the equation of the curve | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
y &= -x^2 + 2x + 2\\[5pt] | y &= -x^2 + 2x + 2\\[5pt] | ||
&= -\bigl(x^2 - 2x- 2\bigr)\\[5pt] | &= -\bigl(x^2 - 2x- 2\bigr)\\[5pt] | ||
| Zeile 16: | Zeile 16: | ||
We can express this area using the integral | We can express this area using the integral | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\text{Area} = \int\limits_a^b \bigl(-x^2+2x+2\bigr)\,dx\,,</math>}} |
where ''a'' and ''b'' are the ''x''-coordinates for the points of intersection between the parabola and the ''x''-axis. | where ''a'' and ''b'' are the ''x''-coordinates for the points of intersection between the parabola and the ''x''-axis. | ||
| Zeile 25: | Zeile 25: | ||
The parabola cuts the ''x''-axis when its ''y''-coordinate is zero, i.e. | The parabola cuts the ''x''-axis when its ''y''-coordinate is zero, i.e. | ||
| - | {{ | + | {{Abgesetzte Formel||<math>0=-x^{2}+2x+2</math>}} |
and because we have already completed the square of the right-hand side once, the equation can be written as | and because we have already completed the square of the right-hand side once, the equation can be written as | ||
| - | {{ | + | {{Abgesetzte Formel||<math>0=-(x-1)^2+3</math>}} |
or | or | ||
| - | {{ | + | {{Abgesetzte Formel||<math>(x-1)^2=3\,\textrm{.}</math>}} |
Taking the square root gives <math>x = 1\pm \sqrt{3}\,</math>. The points of intersection are <math>x=1-\sqrt{3}</math> and <math>x=1+\sqrt{3}\,</math>. | Taking the square root gives <math>x = 1\pm \sqrt{3}\,</math>. The points of intersection are <math>x=1-\sqrt{3}</math> and <math>x=1+\sqrt{3}\,</math>. | ||
| Zeile 39: | Zeile 39: | ||
The area we are looking for is therefore given by | The area we are looking for is therefore given by | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\text{Area} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl(-x^2+2x+2\bigr)\,dx\,\textrm{.}</math>}} |
Instead of directly starting to calculate, we can start from the integrand in the form we obtain after completing its square, | Instead of directly starting to calculate, we can start from the integrand in the form we obtain after completing its square, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\text{Area} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl( -(x-1)^2 + 3\bigr)\,dx\,,</math>}} |
which seems easier. Because the expression <math>x-1</math> inside the square is a linear expression, we can write down a primitive function “in the usual way”, | which seems easier. Because the expression <math>x-1</math> inside the square is a linear expression, we can write down a primitive function “in the usual way”, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\text{Area} = \Bigl[\ -\frac{(x-1)^3}{3} + 3x\ \Bigr]_{1-\sqrt{3}}^{1+\sqrt{3}}\,\textrm{.}</math>}} |
(If one is uncertain of this step, it is possible to differentiate the primitive function and see that one really does get the integrand back). Hence, | (If one is uncertain of this step, it is possible to differentiate the primitive function and see that one really does get the integrand back). Hence, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
\text{Area} &= -\frac{(1+\sqrt{3}-1)^3}{3}+3(1+\sqrt{3}\,)-\Bigl(-\frac{(1-\sqrt{3}-1)^3}{3}+3(1-\sqrt{3}\,)\Bigr)\\[5pt] | \text{Area} &= -\frac{(1+\sqrt{3}-1)^3}{3}+3(1+\sqrt{3}\,)-\Bigl(-\frac{(1-\sqrt{3}-1)^3}{3}+3(1-\sqrt{3}\,)\Bigr)\\[5pt] | ||
&= -\frac{(\sqrt{3}\,)^3}{3} + 3 + 3\sqrt{3} + \frac{(-\sqrt{3}\,)^3}{3} - 3 + 3\sqrt{3}\\[5pt] | &= -\frac{(\sqrt{3}\,)^3}{3} + 3 + 3\sqrt{3} + \frac{(-\sqrt{3}\,)^3}{3} - 3 + 3\sqrt{3}\\[5pt] | ||
| Zeile 64: | Zeile 64: | ||
Note: The calculations become a lot more complicated if one starts from | Note: The calculations become a lot more complicated if one starts from | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\int\limits_{1-\sqrt{3}}^{1+\sqrt{3}}{\bigl(-x^2+2x+2 \bigr)}\,dx = \cdots</math>}} |
Version vom 12:59, 10. Mär. 2009
By completing the square of the equation of the curve
| \displaystyle \begin{align}
y &= -x^2 + 2x + 2\\[5pt] &= -\bigl(x^2 - 2x- 2\bigr)\\[5pt] &= -\bigl((x-1)^2 - 1^2 - 2\bigr)\\[5pt] &= -(x-1)^2 + 3 \end{align} |
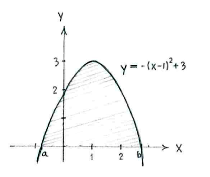
we can read off that the curve is a downward parabola with maximum value \displaystyle y=3 when \displaystyle x=1.
The region whose area we shall determine is the one shaded in the figure.
We can express this area using the integral
| \displaystyle \text{Area} = \int\limits_a^b \bigl(-x^2+2x+2\bigr)\,dx\,, |
where a and b are the x-coordinates for the points of intersection between the parabola and the x-axis.
A solution plan is to first determine the intersection points, \displaystyle x=a and \displaystyle x=b, and then calculate the area using the integral formula above.
The parabola cuts the x-axis when its y-coordinate is zero, i.e.
| \displaystyle 0=-x^{2}+2x+2 |
and because we have already completed the square of the right-hand side once, the equation can be written as
| \displaystyle 0=-(x-1)^2+3 |
or
| \displaystyle (x-1)^2=3\,\textrm{.} |
Taking the square root gives \displaystyle x = 1\pm \sqrt{3}\,. The points of intersection are \displaystyle x=1-\sqrt{3} and \displaystyle x=1+\sqrt{3}\,.
The area we are looking for is therefore given by
| \displaystyle \text{Area} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl(-x^2+2x+2\bigr)\,dx\,\textrm{.} |
Instead of directly starting to calculate, we can start from the integrand in the form we obtain after completing its square,
| \displaystyle \text{Area} = \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}} \bigl( -(x-1)^2 + 3\bigr)\,dx\,, |
which seems easier. Because the expression \displaystyle x-1 inside the square is a linear expression, we can write down a primitive function “in the usual way”,
| \displaystyle \text{Area} = \Bigl[\ -\frac{(x-1)^3}{3} + 3x\ \Bigr]_{1-\sqrt{3}}^{1+\sqrt{3}}\,\textrm{.} |
(If one is uncertain of this step, it is possible to differentiate the primitive function and see that one really does get the integrand back). Hence,
| \displaystyle \begin{align}
\text{Area} &= -\frac{(1+\sqrt{3}-1)^3}{3}+3(1+\sqrt{3}\,)-\Bigl(-\frac{(1-\sqrt{3}-1)^3}{3}+3(1-\sqrt{3}\,)\Bigr)\\[5pt] &= -\frac{(\sqrt{3}\,)^3}{3} + 3 + 3\sqrt{3} + \frac{(-\sqrt{3}\,)^3}{3} - 3 + 3\sqrt{3}\\[5pt] &= -\frac{\sqrt{3}\sqrt{3}\sqrt{3}}{3} + 3\sqrt{3} + \frac{(-\sqrt{3}\,)(-\sqrt{3}\,)(-\sqrt{3}\,)}{3} + 3\sqrt{3}\\[5pt] &= -\frac{3\sqrt{3}}{3} + 3\sqrt{3} - \frac{3\sqrt{3}}{3} + 3\sqrt{3}\\[5pt] &= -\sqrt{3} + 3\sqrt{3} - \sqrt{3} + 3\sqrt{3}\\[5pt] &= (-1+3-1+3)\sqrt{3}\\[5pt] &= 4\sqrt{3}\,\textrm{.} \end{align} |
Note: The calculations become a lot more complicated if one starts from
| \displaystyle \int\limits_{1-\sqrt{3}}^{1+\sqrt{3}}{\bigl(-x^2+2x+2 \bigr)}\,dx = \cdots |