Lösung 1.3:6

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel))
Zeile 1: Zeile 1:
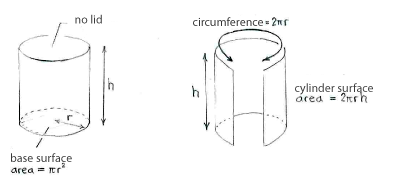
If we call the radius of the metal can ''r'' and its height ''h'', then we can determine the can's volume and area by using the figures below,
If we call the radius of the metal can ''r'' and its height ''h'', then we can determine the can's volume and area by using the figures below,
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
\text{Volume} &= \text{(area of the base)}\cdot\text{(height)}\\[5pt]
\text{Volume} &= \text{(area of the base)}\cdot\text{(height)}\\[5pt]
&= \pi r^2\cdot h\,,\\[10pt]
&= \pi r^2\cdot h\,,\\[10pt]
Zeile 14: Zeile 14:
From the formula for the volume, we can make ''h'' the subject,
From the formula for the volume, we can make ''h'' the subject,
-
{{Displayed math||<math>h=\frac{V}{\pi r^2}</math>}}
+
{{Abgesetzte Formel||<math>h=\frac{V}{\pi r^2}</math>}}
and express the area solely in terms of the radius, ''r'',
and express the area solely in terms of the radius, ''r'',
-
{{Displayed math||<math>A = \pi r^2 + 2\pi r\cdot\frac{V}{\pi r^2} = \pi r^2 + \frac{2V}{r}\,\textrm{.}</math>}}
+
{{Abgesetzte Formel||<math>A = \pi r^2 + 2\pi r\cdot\frac{V}{\pi r^2} = \pi r^2 + \frac{2V}{r}\,\textrm{.}</math>}}
The minimisation problem is then:
The minimisation problem is then:
Zeile 28: Zeile 28:
The derivative is given by
The derivative is given by
-
{{Displayed math||<math>A'(r) = 2\pi r - \frac{2V}{r^2}\,,</math>}}
+
{{Abgesetzte Formel||<math>A'(r) = 2\pi r - \frac{2V}{r^2}\,,</math>}}
and if we set the derivative equal to zero, so as to obtain the critical points, we get
and if we set the derivative equal to zero, so as to obtain the critical points, we get
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
& 2\pi r - \frac{2V}{r^2} = 0\quad \Leftrightarrow \quad 2\pi r = \frac{2V}{r^2}\\[5pt]
& 2\pi r - \frac{2V}{r^2} = 0\quad \Leftrightarrow \quad 2\pi r = \frac{2V}{r^2}\\[5pt]
&\quad\Leftrightarrow \quad r^3=\frac{V}{\pi}\quad \Leftrightarrow \quad r=\sqrt[\scriptstyle 3]{\frac{V}{\pi}}\,\textrm{.}
&\quad\Leftrightarrow \quad r^3=\frac{V}{\pi}\quad \Leftrightarrow \quad r=\sqrt[\scriptstyle 3]{\frac{V}{\pi}}\,\textrm{.}
Zeile 39: Zeile 39:
For this value of ''r'', the second derivative,
For this value of ''r'', the second derivative,
-
{{Displayed math||<math>A''(r) = 2\pi + \frac{4V}{r^3}\,,</math>}}
+
{{Abgesetzte Formel||<math>A''(r) = 2\pi + \frac{4V}{r^3}\,,</math>}}
has the value
has the value
-
{{Displayed math||<math>A''\bigl(\sqrt[3]{V/\pi}\bigr) = 2\pi + \frac{4V}{V/\pi } = 6\pi > 0\,,</math>}}
+
{{Abgesetzte Formel||<math>A''\bigl(\sqrt[3]{V/\pi}\bigr) = 2\pi + \frac{4V}{V/\pi } = 6\pi > 0\,,</math>}}
which shows that <math>r=\sqrt[3]{V/\pi}</math> is a local minimum.
which shows that <math>r=\sqrt[3]{V/\pi}</math> is a local minimum.
Zeile 54: Zeile 54:
The metal can has the least area for a given volume <math>V</math> when
The metal can has the least area for a given volume <math>V</math> when
-
{{Displayed math||<math>\begin{align}
+
{{Abgesetzte Formel||<math>\begin{align}
r &= \sqrt[3]{V/\pi}\,,\quad\text{and}\\[5pt]
r &= \sqrt[3]{V/\pi}\,,\quad\text{and}\\[5pt]
h &= \frac{V}{\pi r^{2}} = \frac{V}{\pi}\Bigl(\frac{V}{\pi}\Bigr)^{-2/3} = \Bigl( \frac{V}{\pi}\Bigr)^{1-2/3} = \Bigl(\frac{V}{\pi}\Bigr)^{1/3} = \sqrt[3]{\frac{V}{\pi}}\,\textrm{.}
h &= \frac{V}{\pi r^{2}} = \frac{V}{\pi}\Bigl(\frac{V}{\pi}\Bigr)^{-2/3} = \Bigl( \frac{V}{\pi}\Bigr)^{1-2/3} = \Bigl(\frac{V}{\pi}\Bigr)^{1/3} = \sqrt[3]{\frac{V}{\pi}}\,\textrm{.}
\end{align}</math>}}
\end{align}</math>}}

Version vom 12:57, 10. Mär. 2009

If we call the radius of the metal can r and its height h, then we can determine the can's volume and area by using the figures below,

\displaystyle \begin{align}

\text{Volume} &= \text{(area of the base)}\cdot\text{(height)}\\[5pt] &= \pi r^2\cdot h\,,\\[10pt] \text{Area} &= \text{(area of the base)} + \text{(area of the cylindrical surface)}\\[5pt] &= \pi r^2 + 2\pi rh\,\textrm{.} \end{align}

The problem can then be formulated as: minimise the can's area, \displaystyle A = \pi r^2 + 2\pi h, whilst at the same time keeping the volume, \displaystyle V = \pi r^2h\,, constant.

From the formula for the volume, we can make h the subject,

\displaystyle h=\frac{V}{\pi r^2}

and express the area solely in terms of the radius, r,

\displaystyle A = \pi r^2 + 2\pi r\cdot\frac{V}{\pi r^2} = \pi r^2 + \frac{2V}{r}\,\textrm{.}

The minimisation problem is then:

Minimise the area \displaystyle A(r) = \pi r^2 + \frac{2V}{r}, when \displaystyle r>0\,.

The area function \displaystyle A(r) is differentiable for all \displaystyle r>0 and the region of definition \displaystyle r>0 has no endpoints (\displaystyle r=0 does not satisfy \displaystyle r>0), so the function can only assume extreme values at critical points.

The derivative is given by

\displaystyle A'(r) = 2\pi r - \frac{2V}{r^2}\,,

and if we set the derivative equal to zero, so as to obtain the critical points, we get

\displaystyle \begin{align}

& 2\pi r - \frac{2V}{r^2} = 0\quad \Leftrightarrow \quad 2\pi r = \frac{2V}{r^2}\\[5pt] &\quad\Leftrightarrow \quad r^3=\frac{V}{\pi}\quad \Leftrightarrow \quad r=\sqrt[\scriptstyle 3]{\frac{V}{\pi}}\,\textrm{.} \end{align}

For this value of r, the second derivative,

\displaystyle A''(r) = 2\pi + \frac{4V}{r^3}\,,

has the value

\displaystyle A''\bigl(\sqrt[3]{V/\pi}\bigr) = 2\pi + \frac{4V}{V/\pi } = 6\pi > 0\,,

which shows that \displaystyle r=\sqrt[3]{V/\pi} is a local minimum.

Because the region of definition, \displaystyle r>0, is open (the endpoint \displaystyle r=0\text{ } is not included) and unlimited, we cannot directly say that the area is least when \displaystyle r = \sqrt[3]{V/\pi}\,; it could be the case that area becomes smaller when \displaystyle r\to 0 or \displaystyle r\to \infty . In this case, however, the area increases without bound as \displaystyle r\to 0 or \displaystyle r\to \infty , so \displaystyle r=\sqrt[3]{V/\pi} really is a global minimum.

The metal can has the least area for a given volume \displaystyle V when

\displaystyle \begin{align}

r &= \sqrt[3]{V/\pi}\,,\quad\text{and}\\[5pt] h &= \frac{V}{\pi r^{2}} = \frac{V}{\pi}\Bigl(\frac{V}{\pi}\Bigr)^{-2/3} = \Bigl( \frac{V}{\pi}\Bigr)^{1-2/3} = \Bigl(\frac{V}{\pi}\Bigr)^{1/3} = \sqrt[3]{\frac{V}{\pi}}\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:6“