Lösung 3.3:2a
Aus Online Mathematik Brückenkurs 2
K |
|||
| Zeile 1: | Zeile 1: | ||
| - | An equation of the type | + | An equation of the type "<math>z^{n} = \text{a complex number}</math>" is called a binomial equation and these are usually solved by going over to polar form and using de Moivre's formula. |
| - | <math>z^{n}</math> | + | |
| - | + | ||
| - | We start by writing | + | We start by writing <math>z</math> and <math>1</math> in polar form |
| - | <math>z | + | |
| - | and | + | |
| - | <math> | + | |
| - | in polar form | + | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | {{Displayed math||<math>\begin{align} | ||
| + | z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] | ||
| + | 1 &= 1(\cos 0 + i\sin 0)\,\textrm{.} | ||
| + | \end{align}</math>}} | ||
The equation then becomes | The equation then becomes | ||
| + | {{Displayed math||<math>r^4(\cos 4\alpha + i\sin 4\alpha) = 1\,(\cos 0 + i\sin 0)\,,</math>}} | ||
| - | <math> | + | where we have used de Moivre's formula on the left-hand side. In order that both sides are equal, they must have the same magnitude and the same argument to within a multiple of <math>2\pi</math>, i.e. |
| - | + | {{Displayed math||<math>\left\{\begin{align} | |
| - | + | r^{4} &= 1\,,\\[5pt] | |
| - | + | 4\alpha &= 0+2n\pi\,,\quad (\text{n is an arbitrary integer})\,\textrm{.} | |
| - | + | \end{align}\right.</math>}} | |
| - | + | ||
| - | <math>\left\{ \begin{ | + | |
| - | r^{4}=1 | + | |
| - | 4\alpha =0+2n\pi \ | + | |
| - | \end{ | + | |
This means that | This means that | ||
| - | + | {{Displayed math||<math>\left\{\begin{align} | |
| - | <math>\left\{ \begin{ | + | r &= 1\,,\\[5pt] |
| - | r=1 | + | \alpha &= \frac{n\pi}{2}\,,\quad \text{(n is an arbitrary integer).} |
| - | \alpha =\frac{n\pi }{2}\quad \ | + | \end{align}\right.</math>}} |
| - | \end{ | + | |
The solutions are thus (in polar form) | The solutions are thus (in polar form) | ||
| + | {{Displayed math||<math>z = 1\cdot\Bigl(\cos\frac{n\pi}{2} + i\sin\frac{n\pi}{2}\Bigr)\,,\quad\text{for }n=0,\ \pm 1,\ \pm 2,\ldots</math>}} | ||
| - | + | but observe that the argument on the right-hand side essentially takes only four different values <math>0</math>, <math>\pi/2</math>, <math>\pi</math> and <math>3\pi/2\,</math>, because other values of <math>n</math> give some of these values plus/minus a multiple of <math>2\pi\,</math>. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | but observe that the argument on the right-hand side essentially takes only four different values | + | |
| - | <math>0, | + | |
| - | and | + | |
| - | <math> | + | |
| - | <math>n | + | |
| - | give some of these values plus/minus a multiple of | + | |
| - | <math>2\pi </math>. | + | |
The equation's solutions are therefore | The equation's solutions are therefore | ||
| + | {{Displayed math||<math>z=\left\{\begin{align} | ||
| + | &1\cdot(\cos 0 + i\sin 0)\,,\\[5pt] | ||
| + | &1\cdot(\cos (\pi/2) + i\sin (\pi/2))\,,\\[5pt] | ||
| + | &1\cdot(\cos \pi + i\sin \pi)\,,\\[5pt] | ||
| + | &1\cdot(\cos (3\pi/2) + i\sin (3\pi/2))\,, | ||
| + | \end{align}\right. | ||
| + | = | ||
| + | \left\{ \begin{align} | ||
| + | 1\,,&\\[5pt] | ||
| + | i\,,&\\[5pt] | ||
| + | -1\,,&\\[5pt] | ||
| + | -i\,\textrm{.}& | ||
| + | \end{align}\right.</math>}} | ||
| - | <math>z=\left\{ \begin{array}{*{35}l} | ||
| - | 1\centerdot \left( \cos 0+i\sin 0 \right) \\ | ||
| - | 1\centerdot \left( \cos {\pi }/{2}\;+i\sin {\pi }/{2}\; \right) \\ | ||
| - | 1\centerdot \left( \cos \pi +i\sin \pi \right) \\ | ||
| - | 1\centerdot \left( \cos {3\pi }/{2}\;+i\sin {3\pi }/{2}\; \right) \\ | ||
| - | \end{array} \right.=\left\{ \begin{matrix} | ||
| - | 1 \\ | ||
| - | i \\ | ||
| - | -1 \\ | ||
| - | -i \\ | ||
| - | \end{matrix} \right.</math> | ||
| - | |||
| - | |||
| - | NOTE: note that if we mark these solutions on the complex number plane, we see that they are corners in a regular quadrilateral. | ||
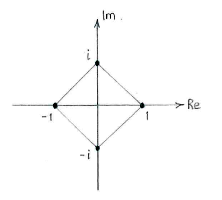
| + | Note: If we mark these solutions on the complex number plane, we see that they are corners in a regular quadrilateral. | ||
[[Image:3_3_2_a.gif|center]] | [[Image:3_3_2_a.gif|center]] | ||
Version vom 11:58, 30. Okt. 2008
An equation of the type "\displaystyle z^{n} = \text{a complex number}" is called a binomial equation and these are usually solved by going over to polar form and using de Moivre's formula.
We start by writing \displaystyle z and \displaystyle 1 in polar form
| \displaystyle \begin{align}
z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] 1 &= 1(\cos 0 + i\sin 0)\,\textrm{.} \end{align} |
The equation then becomes
| \displaystyle r^4(\cos 4\alpha + i\sin 4\alpha) = 1\,(\cos 0 + i\sin 0)\,, |
where we have used de Moivre's formula on the left-hand side. In order that both sides are equal, they must have the same magnitude and the same argument to within a multiple of \displaystyle 2\pi, i.e.
| \displaystyle \left\{\begin{align}
r^{4} &= 1\,,\\[5pt] 4\alpha &= 0+2n\pi\,,\quad (\text{n is an arbitrary integer})\,\textrm{.} \end{align}\right. |
This means that
| \displaystyle \left\{\begin{align}
r &= 1\,,\\[5pt] \alpha &= \frac{n\pi}{2}\,,\quad \text{(n is an arbitrary integer).} \end{align}\right. |
The solutions are thus (in polar form)
| \displaystyle z = 1\cdot\Bigl(\cos\frac{n\pi}{2} + i\sin\frac{n\pi}{2}\Bigr)\,,\quad\text{for }n=0,\ \pm 1,\ \pm 2,\ldots |
but observe that the argument on the right-hand side essentially takes only four different values \displaystyle 0, \displaystyle \pi/2, \displaystyle \pi and \displaystyle 3\pi/2\,, because other values of \displaystyle n give some of these values plus/minus a multiple of \displaystyle 2\pi\,.
The equation's solutions are therefore
| \displaystyle z=\left\{\begin{align}
&1\cdot(\cos 0 + i\sin 0)\,,\\[5pt] &1\cdot(\cos (\pi/2) + i\sin (\pi/2))\,,\\[5pt] &1\cdot(\cos \pi + i\sin \pi)\,,\\[5pt] &1\cdot(\cos (3\pi/2) + i\sin (3\pi/2))\,, \end{align}\right. = \left\{ \begin{align} 1\,,&\\[5pt] i\,,&\\[5pt] -1\,,&\\[5pt] -i\,\textrm{.}& \end{align}\right. |
Note: If we mark these solutions on the complex number plane, we see that they are corners in a regular quadrilateral.