Lösung 3.3:1e

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
One part of the quotient has rather high exponents and this indicates that we ought to use polar form for the calculation.
+
Some parts of the quotient have rather high exponents and this indicates that we ought to use polar form for the calculation.
-
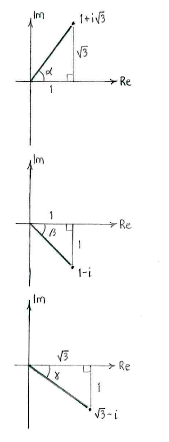
First, we write
+
First, we write <math>1+i\sqrt{3}</math>, <math>1-i</math> and <math>\sqrt{3}-i</math> in polar form.
-
<math>1+i\sqrt{3}</math>,
+
-
<math>\text{1}-i</math>
+
-
and
+
-
<math>\sqrt{3}-i</math>
+
-
in polar form.
+
-
 
+
<center>[[Image:3_3_1_e.gif]] [[Image:3_3_1_e_text.gif]]</center>
-
[[Image:3_3_1_e.gif]] [[Image:3_3_1_e_text.gif]]
+
This shows that
This shows that
-
 
+
{{Displayed math||<math>\begin{align}
-
<math>\begin{align}
+
1+i\sqrt{3} &= 2\Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\,,\\[5pt]
-
& 1+i\sqrt{3}=2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right) \\
+
1-i &= \sqrt{2}\Bigl(\cos\Bigl(-\frac{\pi}{4}\Bigr) + i\sin\Bigl(-\frac{\pi}{4}\Bigr)\Bigr)\,,\\[5pt]
-
& \text{1}-i=\sqrt{2}\left( \cos \left( -\frac{\pi }{4} \right)+i\sin \left( -\frac{\pi }{4} \right) \right) \\
+
\sqrt{3}-i &= 2\Bigl(\cos\Bigl(-\frac{\pi}{6}\Bigr) + i\sin\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)\,\textrm{.}
-
& \sqrt{3}-i=2\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right) \\
+
\end{align}</math>}}
-
\end{align}</math>
+
-
 
+
Now, with the help of de Moivre's formula,
Now, with the help of de Moivre's formula,
-
 
+
{{Displayed math||<math>\begin{align}
-
<math>\begin{align}
+
\frac{\bigl(1+i\sqrt{3}\,\bigr)(1-i)^8}{\bigl(\sqrt{3}-i\bigr)^9}
-
& \frac{\left( 1+i\sqrt{3} \right)\left( \text{1}-i \right)^{8}}{\left( \sqrt{3}-i \right)^{9}}=\frac{2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)\left( \sqrt{2}\left( \cos \left( -\frac{\pi }{4} \right)+i\sin \left( -\frac{\pi }{4} \right) \right) \right)^{8}}{\left( 2\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right) \right)^{9}} \\
+
&= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\Bigl(\sqrt{2}\Bigl(\cos\Bigl(-\dfrac{\pi}{4}\Bigr) + i\sin\Bigl(-\dfrac{\pi}{4}\Bigr)\Bigr)\Bigr)^8}{\Bigl( 2\Bigl(\cos\Bigl(-\dfrac{\pi}{6}\Bigr) + i\sin\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)\Bigr)^9}\\[5pt]
-
& =\frac{2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)\left( \sqrt{2} \right)^{8}\left( \cos \left( 8\centerdot \left( -\frac{\pi }{4} \right) \right)+i\sin \left( 8\centerdot \left( -\frac{\pi }{4} \right) \right) \right)}{2^{9}\left( \cos \left( 9\centerdot \left( -\frac{\pi }{6} \right) \right)+i\sin \left( 9\centerdot \left( -\frac{\pi }{6} \right) \right) \right)} \\
+
&= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\bigl(\sqrt{2}\,\bigr)^8\Bigl(\cos\Bigl(8\cdot\Bigl(-\dfrac{\pi}{4}\Bigr)\Bigr) + i\sin\Bigl(8\cdot\Bigl(-\dfrac{\pi}{4}\Bigr)\Bigr)\Bigr)}{2^{9}\Bigl(\cos\Bigl(9\cdot\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr) + i\sin\Bigl(9\cdot\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)\Bigr)}\\[5pt]
-
& =\frac{2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)\centerdot 2^{\frac{1}{2}\centerdot 8}\left( \cos \left( -2\pi \right)+i\sin \left( -2\pi \right) \right)}{2^{9}\left( \cos \left( -\frac{3\pi }{2} \right)+i\sin \left( -\frac{3\pi }{2} \right) \right)} \\
+
&= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\cdot 2^{(1/2)\cdot 8}\bigl(\cos (-2\pi) + i\sin (-2\pi)\bigr)}{2^9\Bigl(\cos\Bigl(-\dfrac{3\pi}{2} \Bigr) + i\sin\Bigl(-\dfrac{3\pi}{2}\Bigr)\Bigr)}\\[5pt]
-
& =\frac{2\left( \cos \frac{\pi }{3}+i\sin \frac{\pi }{3} \right)\centerdot 2^{4}\left( 1+i\centerdot 0 \right)}{2^{9}\left( \cos \left( -\frac{3\pi }{2} \right)+i\sin \left( -\frac{3\pi }{2} \right) \right)} \\
+
&= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\cdot 2^4( 1+i\cdot 0)}{2^9\Bigl(\cos\Bigl(-\dfrac{3\pi}{2}\Bigr) + i\sin\Bigl(-\dfrac{3\pi}{2}\Bigr)\Bigr)}\\[5pt]
-
& =\frac{2\centerdot 2^{4}}{2^{9}}\left( \cos \left( \frac{\pi }{3}-\left( -\frac{3\pi }{2} \right) \right)+i\sin \left( \frac{\pi }{3}-\left( -\frac{3\pi }{2} \right) \right) \right) \\
+
&= \frac{2\cdot 2^4}{2^9}\Bigl(\cos\Bigl(\frac{\pi}{3}-\Bigl(-\frac{3\pi}{2}\Bigr) \Bigr) + i\sin\Bigl(\frac{\pi}{3}-\Bigl(-\frac{3\pi}{2}\Bigr)\Bigr)\Bigr)\\[5pt]
-
& =\frac{2^{5}}{2^{9}}\left( \cos \left( \frac{\pi }{3}+\frac{3\pi }{2} \right)+i\sin \left( \frac{\pi }{3}+\frac{3\pi }{2} \right) \right) \\
+
&= \frac{2^5}{2^9}\Bigl(\cos\Bigl(\frac{\pi}{3}+\frac{3\pi}{2}\Bigr) + i\sin\Bigl(\frac{\pi}{3}+\frac{3\pi}{2}\Bigr)\Bigr)\\[5pt]
-
& =\frac{1}{2^{4}}\left( \cos \frac{11\pi }{6}+i\sin \frac{11\pi }{6} \right) \\
+
&= \frac{1}{2^4}\Bigl(\cos\frac{11\pi}{6} + i\sin\frac{11\pi}{6}\Bigr)\\[5pt]
-
& =\frac{1}{16}\left( \cos \frac{12\pi -\pi }{6}+i\sin \frac{12\pi -\pi }{6} \right) \\
+
&= \frac{1}{16}\Bigl(\cos\frac{12\pi-\pi}{6} + i\sin\frac{12\pi-\pi}{6}\Bigr)\\[5pt]
-
& =\frac{1}{16}\left( \cos \left( 2\pi -\frac{\pi }{6} \right)+i\sin \left( 2\pi -\frac{\pi }{6} \right) \right) \\
+
&= \frac{1}{16}\Bigl(\cos\Bigl(2\pi-\frac{\pi}{6}\Bigr) + i\sin\Bigl(2\pi-\frac{\pi}{6}\Bigr)\Bigr)\\[5pt]
-
& =\frac{1}{16}\left( \cos \left( -\frac{\pi }{6} \right)+i\sin \left( -\frac{\pi }{6} \right) \right) \\
+
&= \frac{1}{16}\Bigl(\cos\Bigl(-\frac{\pi}{6}\Bigr) + i\sin\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)\\[5pt]
-
& =\frac{1}{16}\left( \frac{\sqrt{3}}{2}-\frac{i}{2} \right)=\frac{1}{32}\left( \sqrt{3}-i \right) \\
+
&= \frac{1}{16}\Bigl(\frac{\sqrt{3}}{2}-\frac{i}{2}\Bigr)\\[5pt]
-
\end{align}</math>
+
&= \frac{1}{32}\bigl(\sqrt{3}-i\bigr)\,\textrm{.}
 +
\end{align}</math>}}

Version vom 09:59, 30. Okt. 2008

Some parts of the quotient have rather high exponents and this indicates that we ought to use polar form for the calculation.

First, we write \displaystyle 1+i\sqrt{3}, \displaystyle 1-i and \displaystyle \sqrt{3}-i in polar form.

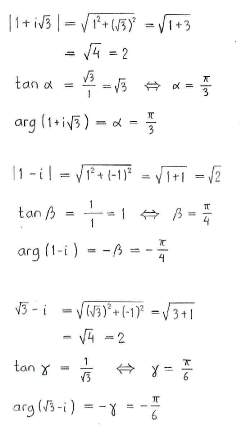
Image:3_3_1_e.gif Image:3_3_1_e_text.gif

This shows that

\displaystyle \begin{align}

1+i\sqrt{3} &= 2\Bigl(\cos\frac{\pi}{3} + i\sin\frac{\pi}{3}\Bigr)\,,\\[5pt] 1-i &= \sqrt{2}\Bigl(\cos\Bigl(-\frac{\pi}{4}\Bigr) + i\sin\Bigl(-\frac{\pi}{4}\Bigr)\Bigr)\,,\\[5pt] \sqrt{3}-i &= 2\Bigl(\cos\Bigl(-\frac{\pi}{6}\Bigr) + i\sin\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)\,\textrm{.} \end{align}

Now, with the help of de Moivre's formula,

\displaystyle \begin{align}

\frac{\bigl(1+i\sqrt{3}\,\bigr)(1-i)^8}{\bigl(\sqrt{3}-i\bigr)^9} &= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\Bigl(\sqrt{2}\Bigl(\cos\Bigl(-\dfrac{\pi}{4}\Bigr) + i\sin\Bigl(-\dfrac{\pi}{4}\Bigr)\Bigr)\Bigr)^8}{\Bigl( 2\Bigl(\cos\Bigl(-\dfrac{\pi}{6}\Bigr) + i\sin\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)\Bigr)^9}\\[5pt] &= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\bigl(\sqrt{2}\,\bigr)^8\Bigl(\cos\Bigl(8\cdot\Bigl(-\dfrac{\pi}{4}\Bigr)\Bigr) + i\sin\Bigl(8\cdot\Bigl(-\dfrac{\pi}{4}\Bigr)\Bigr)\Bigr)}{2^{9}\Bigl(\cos\Bigl(9\cdot\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr) + i\sin\Bigl(9\cdot\Bigl(-\dfrac{\pi}{6}\Bigr)\Bigr)\Bigr)}\\[5pt] &= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\cdot 2^{(1/2)\cdot 8}\bigl(\cos (-2\pi) + i\sin (-2\pi)\bigr)}{2^9\Bigl(\cos\Bigl(-\dfrac{3\pi}{2} \Bigr) + i\sin\Bigl(-\dfrac{3\pi}{2}\Bigr)\Bigr)}\\[5pt] &= \frac{2\Bigl(\cos\dfrac{\pi}{3} + i\sin\dfrac{\pi}{3}\Bigr)\cdot 2^4( 1+i\cdot 0)}{2^9\Bigl(\cos\Bigl(-\dfrac{3\pi}{2}\Bigr) + i\sin\Bigl(-\dfrac{3\pi}{2}\Bigr)\Bigr)}\\[5pt] &= \frac{2\cdot 2^4}{2^9}\Bigl(\cos\Bigl(\frac{\pi}{3}-\Bigl(-\frac{3\pi}{2}\Bigr) \Bigr) + i\sin\Bigl(\frac{\pi}{3}-\Bigl(-\frac{3\pi}{2}\Bigr)\Bigr)\Bigr)\\[5pt] &= \frac{2^5}{2^9}\Bigl(\cos\Bigl(\frac{\pi}{3}+\frac{3\pi}{2}\Bigr) + i\sin\Bigl(\frac{\pi}{3}+\frac{3\pi}{2}\Bigr)\Bigr)\\[5pt] &= \frac{1}{2^4}\Bigl(\cos\frac{11\pi}{6} + i\sin\frac{11\pi}{6}\Bigr)\\[5pt] &= \frac{1}{16}\Bigl(\cos\frac{12\pi-\pi}{6} + i\sin\frac{12\pi-\pi}{6}\Bigr)\\[5pt] &= \frac{1}{16}\Bigl(\cos\Bigl(2\pi-\frac{\pi}{6}\Bigr) + i\sin\Bigl(2\pi-\frac{\pi}{6}\Bigr)\Bigr)\\[5pt] &= \frac{1}{16}\Bigl(\cos\Bigl(-\frac{\pi}{6}\Bigr) + i\sin\Bigl(-\frac{\pi}{6}\Bigr)\Bigr)\\[5pt] &= \frac{1}{16}\Bigl(\frac{\sqrt{3}}{2}-\frac{i}{2}\Bigr)\\[5pt] &= \frac{1}{32}\bigl(\sqrt{3}-i\bigr)\,\textrm{.} \end{align}

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.3:1e“