Lösung 3.2:3

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
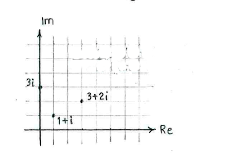
If we mark the three complex numbers in the plane, we see that the fourth corner will have
+
If we mark the three complex numbers in the plane, we see that the fourth corner will have <math>3+2i</math> and <math>3i</math> as neighbouring corners.
-
<math>\text{3}+\text{2}i</math>
+
-
and
+
-
<math>\text{3}i</math>
+
-
as neighbouring corners.
+
-
 
+
[[Image:3_2_3_1.gif|center]]
[[Image:3_2_3_1.gif|center]]
-
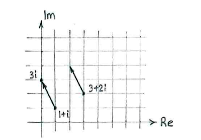
In order to find the fourth corner, we use the fact that in a square opposite sides are parallel and all sides have the same length. This means that the vector from
+
In order to find the fourth corner, we use the fact that in a square opposite sides are parallel and all sides have the same length. This means that the vector from <math>1+i</math> to <math>3i</math> is equal to the vector from <math>3+2i</math> to the fourth corner.
-
<math>\text{1}+i</math>
+
-
to
+
-
<math>\text{3}i</math>
+
-
is equal to the vector from
+
-
<math>\text{3}+\text{2}i</math>
+
-
to the fourth corner.
+
-
 
+
[[Image:3_2_3_2.gif|center]]
[[Image:3_2_3_2.gif|center]]
If we interpret the complex numbers as vectors, this means that the vector from
If we interpret the complex numbers as vectors, this means that the vector from
-
<math>\text{1}+i</math>
+
<math>1+i</math> to <math>\text{3}i</math> is
-
to
+
-
<math>\text{3}i</math>
+
-
is
+
-
 
+
-
 
+
-
<math>3i-\left( 1+i \right)=-1+2i</math>
+
-
 
+
-
And we obtain the fourth corner if we add this vector to the corner
+
{{Displayed math||<math>3i-(1+i) = -1+2i</math>}}
-
<math>\text{3}+\text{2}i</math>,
+
 +
and we obtain the fourth corner if we add this vector to the corner <math>3+2i</math>,
-
<math>\text{3}+\text{2}i+\left( -1+2i \right)=2+4i</math>
+
{{Displayed math||<math>3+2i+(-1+2i) = 2+4i\,\textrm{.}</math>}}

Version vom 09:51, 29. Okt. 2008

If we mark the three complex numbers in the plane, we see that the fourth corner will have \displaystyle 3+2i and \displaystyle 3i as neighbouring corners.

In order to find the fourth corner, we use the fact that in a square opposite sides are parallel and all sides have the same length. This means that the vector from \displaystyle 1+i to \displaystyle 3i is equal to the vector from \displaystyle 3+2i to the fourth corner.

If we interpret the complex numbers as vectors, this means that the vector from \displaystyle 1+i to \displaystyle \text{3}i is

\displaystyle 3i-(1+i) = -1+2i

and we obtain the fourth corner if we add this vector to the corner \displaystyle 3+2i,

\displaystyle 3+2i+(-1+2i) = 2+4i\,\textrm{.}
Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:3“