Lösung 1.3:2c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K
Zeile 1: Zeile 1:
-
There are three types of points at which the function can have local extreme points:
+
There are three types of points at which the function can have local extreme points,
-
1. Critical points, i.e. where
+
# critical points, i.e. where <math>f^{\,\prime}(x)=0</math>,
-
<math>{f}'\left( x \right)=0</math>;
+
# points where the function is not differentiable, and
 +
# endpoints of the interval of definition.
-
2. Points where the function is not differentiable;
+
Because our function is a polynomial, it is defined and differentiable everywhere, and therefore does not have any points which satisfy items 2 and 3.
-
3. Endpoints of the interval of definition.
+
As regards item 1, we set the derivative equal to zero and obtain the equation
-
Because our function is a polynomial, it is defined and differentiable everywhere, and therefore does not have any points which satisfy
+
{{Displayed math||<math>f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}</math>}}
-
<math>2</math>
+
-
and
+
-
<math>3</math>.
+
-
As regards
+
Dividing both sides by 6 and completing the square, we obtain
-
<math>1</math>, we set the derivative equal to zero and obtain the equation
+
-
 
+
{{Displayed math||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}</math>}}
-
<math>{f}'\left( x \right)=6x^{2}+6x-12=0</math>
+
-
 
+
-
Dividing both sides by
+
-
<math>6</math>
+
-
and completing the square, we obtain
+
-
 
+
-
 
+
-
<math>\left( x+\frac{1}{2} \right)^{2}-\left( \frac{1}{2} \right)^{2}-2=0</math>
+
This gives us the equation
This gives us the equation
 +
{{Displayed math||<math>\Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}</math>}}
-
<math>\left( x+\frac{1}{2} \right)^{2}=\frac{9}{4}</math>
+
and taking the square root gives the solutions
 +
{{Displayed math||<math>\begin{align}
 +
x &= -\frac{1}{2}-\sqrt{\frac{9}{4}} = -\frac{1}{2}-\frac{3}{2} = -2\,,\\[5pt]
 +
x &= -\frac{1}{2}+\sqrt{\frac{9}{4}} = -\frac{1}{2}+\frac{3}{2} = 1\,\textrm{.}
 +
\end{align}</math>}}
-
and taking the root gives the solutions
+
This means that if the function has several extreme points, they must be among
 +
<math>x=-2</math> and <math>x=1</math>.
 +
Then, we write down a sign table for the derivative, and read off the possible extreme points.
-
<math>x=-\frac{1}{2}-\sqrt{\frac{9}{4}}=-\frac{1}{2}-\frac{3}{2}=-2</math>
+
{| border="1" cellpadding="5" cellspacing="0" align="center"
 +
|-
 +
|width="50px" align="center" style="background:#efefef;"| <math>x</math>
 +
|width="50px" align="center" style="background:#efefef;"|
 +
|width="50px" align="center" style="background:#efefef;"| <math>-2</math>
 +
|width="50px" align="center" style="background:#efefef;"|
 +
|width="50px" align="center" style="background:#efefef;"| <math>1</math>
 +
|width="50px" align="center" style="background:#efefef;"|
 +
|-
 +
|width="50px" align="center"| <math>f^{\,\prime}(x)</math>
 +
|width="50px" align="center"| <math>+</math>
 +
|width="50px" align="center"| <math>0</math>
 +
|width="50px" align="center"| <math>-</math>
 +
|width="50px" align="center"| <math>0</math>
 +
|width="50px" align="center"| <math>+</math>
 +
|-
 +
|width="50px" align="center"| <math>f(x)</math>
 +
|width="50px" align="center"| <math>\nearrow</math>
 +
|width="50px" align="center"| <math>21</math>
 +
|width="50px" align="center"| <math>\searrow</math>
 +
|width="50px" align="center"| <math>-6</math>
 +
|width="50px" align="center"| <math>\nearrow</math>
 +
|}
-
<math>x=-\frac{1}{2}+\sqrt{\frac{9}{4}}=-\frac{1}{2}+\frac{3}{2}=1</math>
+
The function has a local maximum at <math>x=-2</math> and a local minimum at <math>x=1</math>.
-
 
+
-
 
+
-
This means that if the function has several extreme points, they must lie between
+
-
<math>x=-2\text{ }</math>
+
-
and
+
-
<math>x=1</math>.
+
-
 
+
-
Then, we write down a sign table for the derivative, and read off the possible extreme points.
+
-
 
+
-
TABLE
+
-
 
+
-
The function has a local maximum at
+
-
<math>x=-2\text{ }</math>
+
-
and a local minimum at
+
-
<math>x=1</math>.
+
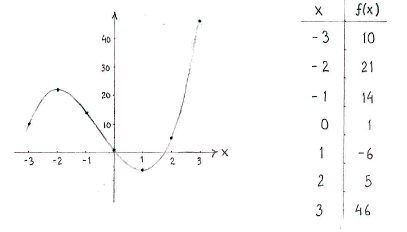
We obtain the overall appearance of the graph of the function from the table and by calculating the value of the function at a few points.
We obtain the overall appearance of the graph of the function from the table and by calculating the value of the function at a few points.
- 
-
PICTURE TABLE
 
- 
- 
[[Image:1_3_2_c.gif|center]]
[[Image:1_3_2_c.gif|center]]

Version vom 12:59, 17. Okt. 2008

There are three types of points at which the function can have local extreme points,

  1. critical points, i.e. where \displaystyle f^{\,\prime}(x)=0,
  2. points where the function is not differentiable, and
  3. endpoints of the interval of definition.

Because our function is a polynomial, it is defined and differentiable everywhere, and therefore does not have any points which satisfy items 2 and 3.

As regards item 1, we set the derivative equal to zero and obtain the equation

\displaystyle f^{\,\prime}(x) = 6x^2+6x-12 = 0\,\textrm{.}

Dividing both sides by 6 and completing the square, we obtain

\displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 - \Bigl(\frac{1}{2}\Bigr)^2 - 2 = 0\,\textrm{.}

This gives us the equation

\displaystyle \Bigl(x+\frac{1}{2}\Bigr)^2 = \frac{9}{4}

and taking the square root gives the solutions

\displaystyle \begin{align}

x &= -\frac{1}{2}-\sqrt{\frac{9}{4}} = -\frac{1}{2}-\frac{3}{2} = -2\,,\\[5pt] x &= -\frac{1}{2}+\sqrt{\frac{9}{4}} = -\frac{1}{2}+\frac{3}{2} = 1\,\textrm{.} \end{align}

This means that if the function has several extreme points, they must be among \displaystyle x=-2 and \displaystyle x=1.

Then, we write down a sign table for the derivative, and read off the possible extreme points.

\displaystyle x \displaystyle -2 \displaystyle 1
\displaystyle f^{\,\prime}(x) \displaystyle + \displaystyle 0 \displaystyle - \displaystyle 0 \displaystyle +
\displaystyle f(x) \displaystyle \nearrow \displaystyle 21 \displaystyle \searrow \displaystyle -6 \displaystyle \nearrow


The function has a local maximum at \displaystyle x=-2 and a local minimum at \displaystyle x=1.

We obtain the overall appearance of the graph of the function from the table and by calculating the value of the function at a few points.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:2c“