Lösung 1.3:6
Aus Online Mathematik Brückenkurs 2
K (Lösning 1.3:6 moved to Solution 1.3:6: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | If we call the radius of the metal can | |
| - | < | + | <math>r</math> |
| - | + | and its height | |
| - | + | <math>h</math>, then we can determine the can's volume and area by using the figures below. | |
| - | < | + | |
| - | + | Volume = (area of the base). (height) | |
| - | + | ||
| - | + | <math>=\pi r^{2}h</math> | |
| - | { | + | |
| - | + | Area= (area of the base)+(area of the cylindrical surface) | |
| - | + | ||
| - | + | <math>=\pi r^{2}+2\pi h</math> | |
| + | |||
[[Image:1_3_6_1.gif|center]] | [[Image:1_3_6_1.gif|center]] | ||
| + | |||
| + | |||
| + | The problem can then be formulated as: minimise the can's area, | ||
| + | <math>A=\pi r^{2}+2\pi h</math>, whilst at the same time keeping the volume, | ||
| + | <math>V=\pi r^{2}h</math>, constant. | ||
| + | |||
| + | From the formula for the volume, we can make | ||
| + | <math>h</math> | ||
| + | the subject, | ||
| + | |||
| + | |||
| + | <math>h=\frac{V}{\pi r^{2}}</math> | ||
| + | |||
| + | |||
| + | and express the area solely in terms of the radius, | ||
| + | <math>r</math>: | ||
| + | |||
| + | |||
| + | <math>A=\pi r^{2}+2\pi r\bullet \frac{V}{\pi r^{2}}=\pi r^{2}+\frac{2V}{r}</math> | ||
| + | |||
| + | |||
| + | The minimisation problem is then: | ||
| + | |||
| + | to minimise the area | ||
| + | <math>A\left( r \right)=\pi r^{2}+\frac{2V}{r}</math> | ||
| + | A(r)=..., when | ||
| + | <math>r>0</math>. | ||
| + | |||
| + | The area function | ||
| + | <math>A\left( r \right)</math> | ||
| + | is differentiable for all | ||
| + | <math>r>0</math> | ||
| + | and the region of definition | ||
| + | <math>r>0</math> | ||
| + | has no endpoints | ||
| + | ( | ||
| + | <math>r=0\text{ }</math> | ||
| + | does not satisfy | ||
| + | <math>r>0</math> | ||
| + | ), so the function can only assume extreme values at critical points. | ||
| + | |||
| + | The derivative is given by | ||
| + | |||
| + | |||
| + | <math>{A}'\left( r \right)=2\pi r-\frac{2V}{r^{2}}</math>, | ||
| + | |||
| + | and if we set the derivative equal to zero, so as to obtain the critical points, we get | ||
| + | |||
| + | <math>\begin{align} | ||
| + | & 2\pi r-\frac{2V}{r^{2}}=0\quad \Leftrightarrow \quad 2\pi r=\frac{2V}{r^{2}} \\ | ||
| + | & \Leftrightarrow \quad r^{3}=\frac{V}{\pi }\quad \Leftrightarrow \quad r=\sqrt[3]{\frac{V}{\pi }} \\ | ||
| + | \end{align}</math> | ||
| + | |||
| + | |||
| + | |||
| + | For this value of | ||
| + | <math>r</math>, the second derivative, | ||
| + | |||
| + | |||
| + | <math>{A}''\left( r \right)=2\pi +\frac{4V}{r^{3}}</math>, | ||
| + | has the value | ||
| + | |||
| + | |||
| + | <math>{A}''\left( \sqrt[3]{\frac{V}{\pi }} \right)=2\pi +\frac{4V}{\frac{V}{\pi }}=6\pi >0</math>, | ||
| + | |||
| + | which shows that | ||
| + | <math>r=\sqrt[3]{{V}/{\pi }\;}</math> | ||
| + | is a local minimum. | ||
| + | |||
| + | Because the region of definition, | ||
| + | <math>r>0</math>, is open (the endpoint | ||
| + | <math>r=0\text{ }</math> | ||
| + | is not included) and unlimited, we cannot directly say that the area is least when | ||
| + | <math>r=\sqrt[3]{{V}/{\pi }\;}</math>; it could be the case that area becomes smaller when | ||
| + | <math>r\to 0</math> | ||
| + | or | ||
| + | <math>r\to \infty </math>. In this case, however, the area increases without bound as | ||
| + | <math>r\to 0</math> | ||
| + | or | ||
| + | <math>r\to \infty </math>, so | ||
| + | <math>r=\sqrt[3]{{V}/{\pi }\;}</math> | ||
| + | really is a global minimum. | ||
| + | |||
| + | The metal can has the least area for a given volume | ||
| + | <math>V</math> | ||
| + | when | ||
| + | |||
| + | |||
| + | <math>r=\sqrt[3]{{V}/{\pi }\;}</math>, and | ||
| + | |||
| + | <math>h=\frac{V}{\pi r^{2}}=\frac{V}{\pi }\left( \frac{V}{\pi } \right)^{-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{1-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{{1}/{3}\;}=\sqrt[3]{\frac{V}{\pi }}</math> | ||
Version vom 13:35, 16. Okt. 2008
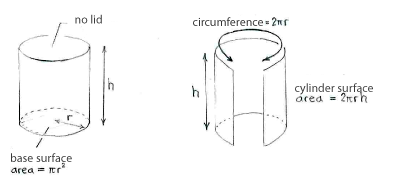
If we call the radius of the metal can \displaystyle r and its height \displaystyle h, then we can determine the can's volume and area by using the figures below.
Volume = (area of the base). (height)
\displaystyle =\pi r^{2}h
Area= (area of the base)+(area of the cylindrical surface)
\displaystyle =\pi r^{2}+2\pi h
The problem can then be formulated as: minimise the can's area,
\displaystyle A=\pi r^{2}+2\pi h, whilst at the same time keeping the volume,
\displaystyle V=\pi r^{2}h, constant.
From the formula for the volume, we can make \displaystyle h the subject,
\displaystyle h=\frac{V}{\pi r^{2}}
and express the area solely in terms of the radius,
\displaystyle r:
\displaystyle A=\pi r^{2}+2\pi r\bullet \frac{V}{\pi r^{2}}=\pi r^{2}+\frac{2V}{r}
The minimisation problem is then:
to minimise the area \displaystyle A\left( r \right)=\pi r^{2}+\frac{2V}{r} A(r)=..., when \displaystyle r>0.
The area function \displaystyle A\left( r \right) is differentiable for all \displaystyle r>0 and the region of definition \displaystyle r>0 has no endpoints ( \displaystyle r=0\text{ } does not satisfy \displaystyle r>0 ), so the function can only assume extreme values at critical points.
The derivative is given by
\displaystyle {A}'\left( r \right)=2\pi r-\frac{2V}{r^{2}},
and if we set the derivative equal to zero, so as to obtain the critical points, we get
\displaystyle \begin{align} & 2\pi r-\frac{2V}{r^{2}}=0\quad \Leftrightarrow \quad 2\pi r=\frac{2V}{r^{2}} \\ & \Leftrightarrow \quad r^{3}=\frac{V}{\pi }\quad \Leftrightarrow \quad r=\sqrt[3]{\frac{V}{\pi }} \\ \end{align}
For this value of \displaystyle r, the second derivative,
\displaystyle {A}''\left( r \right)=2\pi +\frac{4V}{r^{3}},
has the value
\displaystyle {A}''\left( \sqrt[3]{\frac{V}{\pi }} \right)=2\pi +\frac{4V}{\frac{V}{\pi }}=6\pi >0,
which shows that \displaystyle r=\sqrt[3]{{V}/{\pi }\;} is a local minimum.
Because the region of definition, \displaystyle r>0, is open (the endpoint \displaystyle r=0\text{ } is not included) and unlimited, we cannot directly say that the area is least when \displaystyle r=\sqrt[3]{{V}/{\pi }\;}; it could be the case that area becomes smaller when \displaystyle r\to 0 or \displaystyle r\to \infty . In this case, however, the area increases without bound as \displaystyle r\to 0 or \displaystyle r\to \infty , so \displaystyle r=\sqrt[3]{{V}/{\pi }\;} really is a global minimum.
The metal can has the least area for a given volume \displaystyle V when
\displaystyle r=\sqrt[3]{{V}/{\pi }\;}, and
\displaystyle h=\frac{V}{\pi r^{2}}=\frac{V}{\pi }\left( \frac{V}{\pi } \right)^{-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{1-{2}/{3}\;}=\left( \frac{V}{\pi } \right)^{{1}/{3}\;}=\sqrt[3]{\frac{V}{\pi }}