Lösung 3.2:2b
Aus Online Mathematik Brückenkurs 2
K (Lösning 3.2:2b moved to Solution 3.2:2b: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
{{NAVCONTENT_START}} | {{NAVCONTENT_START}} | ||
| - | < | + | The inequality <math>0\leq \mathrm{Re}z \leq \mathrm{Im}z \leq 1</math> is actually several inequalities: |
| - | + | ||
| - | { | + | |
| - | < | + | |
| - | + | ||
| + | <math>\begin{align} | ||
| + | 0 &\leq \mathrm{Re}z \leq 1,\\ | ||
| + | 0 &\leq \mathrm{Im}z \leq 1,\end{align} | ||
| + | |||
| + | \mathrm{Re}z \leq \mathrm{Im}z. | ||
| + | </math> | ||
| + | |||
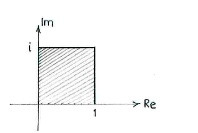
| + | The first two inequalities in this list define the unit square in the complex number plane. | ||
[[Image:3_2_2_b1.gif|center]] | [[Image:3_2_2_b1.gif|center]] | ||
| + | |||
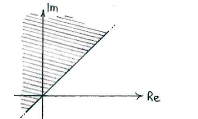
| + | The last inequality says that the real part of <math>z</math> should be less than or equal to the imaginary part of <math>z</math>, I.e. <math>z</math> should lie to the left of the line <math>y=x</math> if <math>x=\mathrm{Re} z</math> and <math>y = \mathrm{Im} z</math>. | ||
| + | |||
[[Image:3_2_2_b2.gif|center]] | [[Image:3_2_2_b2.gif|center]] | ||
| + | |||
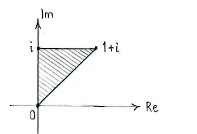
| + | All together, the inequalities define the region which the unit square and the half-plane have in common: a triangle with corner points at <math>0</math>, <math>i</math> and <math>1+i</math>. | ||
| + | |||
[[Image:3_2_2_b3.gif|center]] | [[Image:3_2_2_b3.gif|center]] | ||
| + | |||
| + | {{NAVCONTENT_STOP}} | ||
Version vom 10:49, 3. Okt. 2008
The inequality \displaystyle 0\leq \mathrm{Re}z \leq \mathrm{Im}z \leq 1 is actually several inequalities:
\displaystyle \begin{align} 0 &\leq \mathrm{Re}z \leq 1,\\ 0 &\leq \mathrm{Im}z \leq 1,\end{align}
\mathrm{Re}z \leq \mathrm{Im}z.
The first two inequalities in this list define the unit square in the complex number plane.
The last inequality says that the real part of \displaystyle z should be less than or equal to the imaginary part of \displaystyle z, I.e. \displaystyle z should lie to the left of the line \displaystyle y=x if \displaystyle x=\mathrm{Re} z and \displaystyle y = \mathrm{Im} z.
All together, the inequalities define the region which the unit square and the half-plane have in common: a triangle with corner points at \displaystyle 0, \displaystyle i and \displaystyle 1+i.