Lösung 1.3:5
Aus Online Mathematik Brückenkurs 2
| Zeile 16: | Zeile 16: | ||
Begrenzen wir den Winkel so, dass er zwischen <math>0</math> und <math>\pi/2</math> liegt, erhalten wir das Problem: | Begrenzen wir den Winkel so, dass er zwischen <math>0</math> und <math>\pi/2</math> liegt, erhalten wir das Problem: | ||
| - | ::Maximiere <math>A(\alpha) = 100\cos\alpha (1+\sin\alpha)</math> wenn | + | ::Maximiere <math>A(\alpha) = 100\cos\alpha (1+\sin\alpha)</math> wenn <math>0\le \alpha \le {\pi }/{2}\,</math>. |
| - | <math>0\le \alpha \le {\pi }/{2}\,</math>. | + | |
| - | Die Funktion ist überall differenzierbar | + | Die Funktion ist überall differenzierbar und die Fläche ist minimal wenn <math>\alpha=0</math> oder wenn <math>\alpha=\pi/2\,</math>, also nimmt die Funktion ihr Maximum für einen stationären Punkt an. |
Die Ableitung ist | Die Ableitung ist | ||
| Zeile 28: | Zeile 27: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
| - | Für stationäre Punkte ist <math>A'(\alpha)=0</math> | + | Für stationäre Punkte ist <math>A'(\alpha)=0\,.</math> Das ergibt die Gleichung |
| - | {{Abgesetzte Formel||<math>\sin\alpha + \sin^2\!\alpha - \cos^2\!\alpha = 0</math>}} | + | {{Abgesetzte Formel||<math>\sin\alpha + \sin^2\!\alpha - \cos^2\!\alpha = 0\,.</math>}} |
| - | Nachdem wir den Faktor -100 heraus gezogen haben | + | Nachdem wir den Faktor -100 heraus gezogen haben, ersetzen wir <math>\cos^2\!\alpha</math> mit <math>1-\sin^2\!\alpha</math> und erhalten eine Gleichung mit nur <math>\sin\alpha\,</math>-Termen. |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
\sin\alpha + \sin^2\!\alpha - (1-\sin^2\!\alpha) &= 0\\[5pt] | \sin\alpha + \sin^2\!\alpha - (1-\sin^2\!\alpha) &= 0\\[5pt] | ||
| - | 2\sin^2\!\alpha + \sin\alpha - 1 &= 0\,\textrm{ | + | 2\sin^2\!\alpha + \sin\alpha - 1 &= 0\,\textrm{} |
\end{align}</math>}} | \end{align}</math>}} | ||
| - | + | Das ist eine quadratische Gleichung für <math>\sin\alpha</math>. Durch quadratische Ergänzung erhalten wir | |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
2\bigl(\sin\alpha + \tfrac{1}{4}\bigr)^{2} - 2\bigl(\tfrac{1}{4}\bigr)^2 - 1 &= 0\\[5pt] | 2\bigl(\sin\alpha + \tfrac{1}{4}\bigr)^{2} - 2\bigl(\tfrac{1}{4}\bigr)^2 - 1 &= 0\\[5pt] | ||
\bigl(\sin\alpha + \tfrac{1}{4}\bigr)^2 &= \frac{9}{16} | \bigl(\sin\alpha + \tfrac{1}{4}\bigr)^2 &= \frac{9}{16} | ||
| - | \end{align}</math>}} | + | \end{align}</math>.}} |
| - | + | Wir erhalten weiter <math>\sin\alpha = -\tfrac{1}{4}\pm \tfrac{3}{4}</math>, also <math>\sin \alpha = -1</math> oder <math>\sin \alpha = \tfrac{1}{2}\,</math>. | |
| - | Der Fall dass <math>\sin \alpha =-1</math> ist nie erfüllt für <math>0\le \alpha \le \pi/2</math> und <math>\sin \alpha = \tfrac{1}{2}</math> gibt <math>\alpha = \pi/6</math>. Also ist <math>\alpha = \pi/6\,</math> ein stationärer Punkt. | + | Der Fall, dass <math>\sin \alpha =-1</math>, ist nie erfüllt für <math>0\le \alpha \le \pi/2</math> und <math>\sin \alpha = \tfrac{1}{2}</math> gibt <math>\alpha = \pi/6</math>. Also ist <math>\alpha = \pi/6\,</math> ein stationärer Punkt. |
| - | Wir wissen von der Figur her dass die Fläche lokale Minima in den Punkten <math>\alpha = 0</math> und <math>\alpha = \pi/2</math> hat | + | Wir wissen von der Figur her, dass die Fläche lokale Minima in den Punkten <math>\alpha = 0</math> und <math>\alpha = \pi/2</math> hat und den kritischen Punkt <math>\alpha = \pi/6\,</math>. Daher muss der kritische Punkt ein Maximum sein, wir zeigen dies mit der zweiten Ableitung. |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
A''(\alpha) &= -100\cos\alpha - 100\cdot 2\sin\alpha\cdot\cos\alpha + 100\cdot 2\cos\alpha \cdot (-\sin\alpha)\\[5pt] | A''(\alpha) &= -100\cos\alpha - 100\cdot 2\sin\alpha\cdot\cos\alpha + 100\cdot 2\cos\alpha \cdot (-\sin\alpha)\\[5pt] | ||
| - | &= -100\cos\alpha (1+4\sin\alpha)\, | + | &= -100\cos\alpha (1+4\sin\alpha)\,. |
\end{align}</math>}} | \end{align}</math>}} | ||
| - | Dieser Ausdruck ist negativ für <math>\alpha = \pi/6</math> | + | Dieser Ausdruck ist negativ für <math>\alpha = \pi/6</math>. |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
A''(\pi/6) &= -100\cos\frac{\pi}{6}\cdot \Bigl(1+4\sin\frac{\pi}{6}\Bigr)\\[5pt] | A''(\pi/6) &= -100\cos\frac{\pi}{6}\cdot \Bigl(1+4\sin\frac{\pi}{6}\Bigr)\\[5pt] | ||
| - | &= -100\cdot\frac{\sqrt{3}}{2}\cdot \Bigl( 1+4\cdot \frac{1}{2} \Bigr)<0\,\textrm{ | + | &= -100\cdot\frac{\sqrt{3}}{2}\cdot \Bigl( 1+4\cdot \frac{1}{2} \Bigr)<0\,\textrm{} |
\end{align}</math>}} | \end{align}</math>}} | ||
| - | Also ist <math>\alpha = \pi/6\,</math> ein globales Maximum, | + | Also ist <math>\alpha = \pi/6\,</math> ein globales Maximum, da es das einzige lokale Maximum ist. |
Version vom 14:18, 20. Aug. 2009
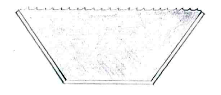
Der Kanal kann am meisten Wasser enthalten, wenn seine Querschnittsfläche am größten ist.
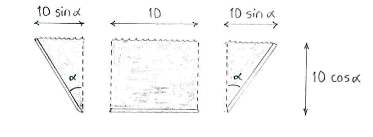
Indem wir den Querschnitt des Kanals in ein Rechteck und zwei Dreiecke aufteilen, können wir mit ein wenig Trigonometrie, die Querschnittsfläche des Kanals berechnen.
Die Fläche ist
| \displaystyle \begin{align}
A(\alpha) &= 10\cdot 10\cos\alpha + 2\cdot\frac{1}{2}\cdot 10\cos\alpha \cdot 10\sin\alpha\\[5pt] &= 100\cos \alpha (1+\sin\alpha)\,\textrm{.} \end{align} |
Begrenzen wir den Winkel so, dass er zwischen \displaystyle 0 und \displaystyle \pi/2 liegt, erhalten wir das Problem:
- Maximiere \displaystyle A(\alpha) = 100\cos\alpha (1+\sin\alpha) wenn \displaystyle 0\le \alpha \le {\pi }/{2}\,.
Die Funktion ist überall differenzierbar und die Fläche ist minimal wenn \displaystyle \alpha=0 oder wenn \displaystyle \alpha=\pi/2\,, also nimmt die Funktion ihr Maximum für einen stationären Punkt an.
Die Ableitung ist
| \displaystyle \begin{align}
A'(\alpha) &= 100\cdot (-\sin\alpha)\cdot (1+\sin\alpha) + 100\cdot\cos\alpha \cdot \cos\alpha\\[5pt] &= -100\sin\alpha - 100\sin^2\!\alpha + 100\cos^2\!\alpha\,\textrm{.} \end{align} |
Für stationäre Punkte ist \displaystyle A'(\alpha)=0\,. Das ergibt die Gleichung
| \displaystyle \sin\alpha + \sin^2\!\alpha - \cos^2\!\alpha = 0\,. |
Nachdem wir den Faktor -100 heraus gezogen haben, ersetzen wir \displaystyle \cos^2\!\alpha mit \displaystyle 1-\sin^2\!\alpha und erhalten eine Gleichung mit nur \displaystyle \sin\alpha\,-Termen.
| \displaystyle \begin{align}
\sin\alpha + \sin^2\!\alpha - (1-\sin^2\!\alpha) &= 0\\[5pt] 2\sin^2\!\alpha + \sin\alpha - 1 &= 0\,\textrm{} \end{align} |
Das ist eine quadratische Gleichung für \displaystyle \sin\alpha. Durch quadratische Ergänzung erhalten wir
| \displaystyle \begin{align}
2\bigl(\sin\alpha + \tfrac{1}{4}\bigr)^{2} - 2\bigl(\tfrac{1}{4}\bigr)^2 - 1 &= 0\\[5pt] \bigl(\sin\alpha + \tfrac{1}{4}\bigr)^2 &= \frac{9}{16} \end{align} . |
Wir erhalten weiter \displaystyle \sin\alpha = -\tfrac{1}{4}\pm \tfrac{3}{4}, also \displaystyle \sin \alpha = -1 oder \displaystyle \sin \alpha = \tfrac{1}{2}\,.
Der Fall, dass \displaystyle \sin \alpha =-1, ist nie erfüllt für \displaystyle 0\le \alpha \le \pi/2 und \displaystyle \sin \alpha = \tfrac{1}{2} gibt \displaystyle \alpha = \pi/6. Also ist \displaystyle \alpha = \pi/6\, ein stationärer Punkt.
Wir wissen von der Figur her, dass die Fläche lokale Minima in den Punkten \displaystyle \alpha = 0 und \displaystyle \alpha = \pi/2 hat und den kritischen Punkt \displaystyle \alpha = \pi/6\,. Daher muss der kritische Punkt ein Maximum sein, wir zeigen dies mit der zweiten Ableitung.
| \displaystyle \begin{align}
A''(\alpha) &= -100\cos\alpha - 100\cdot 2\sin\alpha\cdot\cos\alpha + 100\cdot 2\cos\alpha \cdot (-\sin\alpha)\\[5pt] &= -100\cos\alpha (1+4\sin\alpha)\,. \end{align} |
Dieser Ausdruck ist negativ für \displaystyle \alpha = \pi/6.
| \displaystyle \begin{align}
A''(\pi/6) &= -100\cos\frac{\pi}{6}\cdot \Bigl(1+4\sin\frac{\pi}{6}\Bigr)\\[5pt] &= -100\cdot\frac{\sqrt{3}}{2}\cdot \Bigl( 1+4\cdot \frac{1}{2} \Bigr)<0\,\textrm{} \end{align} |
Also ist \displaystyle \alpha = \pi/6\, ein globales Maximum, da es das einzige lokale Maximum ist.