Lösung 1.3:1a
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
| Zeile 1: | Zeile 1: | ||
| - | Ein stationärer Punkt ist ein Punkt wo die Ableitung der Funktion null ist. | + | Ein stationärer Punkt ist ein Punkt, wo die Ableitung der Funktion null ist. Das entspricht also dem Punkt <math>x=0</math>. |
[[Image:1_3_1_a2.gif|center]] | [[Image:1_3_1_a2.gif|center]] | ||
| - | Noch dazu ist der Punkt <math>x=0</math> ein lokales und globales | + | Noch dazu ist der Punkt <math>x=0</math> ein lokales und globales Maximum, da es keine anderen Punkte mit einem höheren Funktionswert gibt. Es gibt keine Sattelpunkte. |
| - | Links von <math>x=0</math> ist die Ableitung | + | Links von <math>x=0</math> ist die Ableitung negativ und daher ist die Funktion streng fallend. Rechts von <math>x=0</math> ist die Ableitung positiv und daher ist die Funktion streng steigend. |
[[Image:1_3_1_a3_de.gif|center]] | [[Image:1_3_1_a3_de.gif|center]] | ||
Version vom 11:30, 20. Aug. 2009
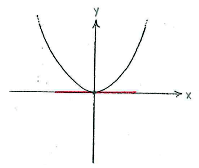
Ein stationärer Punkt ist ein Punkt, wo die Ableitung der Funktion null ist. Das entspricht also dem Punkt \displaystyle x=0.
Noch dazu ist der Punkt \displaystyle x=0 ein lokales und globales Maximum, da es keine anderen Punkte mit einem höheren Funktionswert gibt. Es gibt keine Sattelpunkte.
Links von \displaystyle x=0 ist die Ableitung negativ und daher ist die Funktion streng fallend. Rechts von \displaystyle x=0 ist die Ableitung positiv und daher ist die Funktion streng steigend.