Lösung 3.2:2e

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 3.2:2e moved to Lösung 3.2:2e: Robot: moved page)
Zeile 1: Zeile 1:
-
Because the expression contains both <math>z</math> and <math>\bar{z}</math>, we write out <math>z=x+iy</math>, where <math>x</math> is the real part of <math>z</math> and <math>y</math> is the imaginary part. Thus, we have
+
Nachdem die Gleichung <math>z</math> und <math>\bar{z}</math> enthält, schreiben wir <math>z=x+iy</math>, wo <math>x</math> der Realteil von <math>z</math> ist, und <math>y</math> der Imaginärteil ist. Wir erhalten also
:*<math>\mathop{\rm Re}z = x</math>
:*<math>\mathop{\rm Re}z = x</math>
:*<math>i+\bar{z} = i+(x-iy) = x+(1-y)i</math>
:*<math>i+\bar{z} = i+(x-iy) = x+(1-y)i</math>
-
and the condition becomes
+
Und unsere Gleichung bekommt
{{Abgesetzte Formel||<math>x=x+(1-y)i\quad\Leftrightarrow\quad 0=(1-y)i</math>}}
{{Abgesetzte Formel||<math>x=x+(1-y)i\quad\Leftrightarrow\quad 0=(1-y)i</math>}}
-
which means that <math>y=1</math>.
+
und also ist <math>y=1</math>.
-
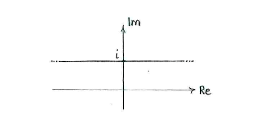
The set therefore consists of all complex numbers with imaginary part 1.
+
Also besteht unsere Fläche aus allen komlexen Zahlen deren Imaginärteil 1 ist.
[[Image:3_2_2_e.gif|center]]
[[Image:3_2_2_e.gif|center]]

Version vom 18:55, 12. Mai 2009

Nachdem die Gleichung \displaystyle z und \displaystyle \bar{z} enthält, schreiben wir \displaystyle z=x+iy, wo \displaystyle x der Realteil von \displaystyle z ist, und \displaystyle y der Imaginärteil ist. Wir erhalten also

  • \displaystyle \mathop{\rm Re}z = x
  • \displaystyle i+\bar{z} = i+(x-iy) = x+(1-y)i

Und unsere Gleichung bekommt

\displaystyle x=x+(1-y)i\quad\Leftrightarrow\quad 0=(1-y)i

und also ist \displaystyle y=1.

Also besteht unsere Fläche aus allen komlexen Zahlen deren Imaginärteil 1 ist.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:2e“