Lösung 3.2:1d

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 3.2:1d moved to Lösung 3.2:1d: Robot: moved page)
Zeile 1: Zeile 1:
-
If we calculate the expression, we get the answer at once,
+
Berechnen wir den Punkt, erhalten wir direkt
{{Abgesetzte Formel||<math>\begin{align}
{{Abgesetzte Formel||<math>\begin{align}
Zeile 8: Zeile 8:
\end{align}</math>}}
\end{align}</math>}}
-
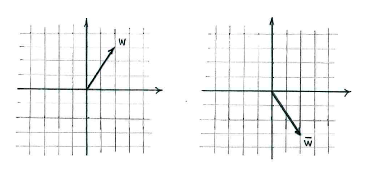
If, on the other hand, we interpret the expression in terms of vectors, we must first understand the vector <math>\bar{w}</math> geometrically. When we take the complex conjugate of <math>w</math>, we change the sign of the imaginary part, which is the same as reflecting <math>w</math> in the real axis.
+
Um den Vektor <math>\bar{w}</math> geometrisch zu deuten, müssen wir einsehen dass die komplexe Konjugation von <math>w</math> eine Spiegelung in der reellen Achse ist, nachdem der Imaginärteil durch die Kunjugation Vorzeichen tauscht.
[[Image:3_2_1_d1.gif|center]]
[[Image:3_2_1_d1.gif|center]]
-
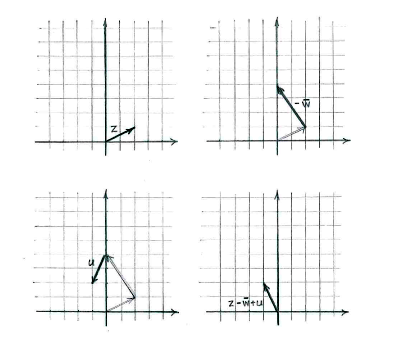
We can then construct the expression <math>z-\bar{w}+u</math> one term at a time.
+
Dadurch erhalten wir den Ausdruck einfach:
[[Image:3_2_1d-2(2).gif|center]]
[[Image:3_2_1d-2(2).gif|center]]

Version vom 18:43, 12. Mai 2009

Berechnen wir den Punkt, erhalten wir direkt

\displaystyle \begin{align}

z-\bar{w}+u &= (2+i)-(2-3i)+(-1-2i)\\[5pt] &= 2-2-1+(1+3-2)i\\[5pt] &= -1+2i\,\textrm{.} \end{align}

Um den Vektor \displaystyle \bar{w} geometrisch zu deuten, müssen wir einsehen dass die komplexe Konjugation von \displaystyle w eine Spiegelung in der reellen Achse ist, nachdem der Imaginärteil durch die Kunjugation Vorzeichen tauscht.

Dadurch erhalten wir den Ausdruck einfach:

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_3.2:1d“