Lösung 1.3:7
Aus Online Mathematik Brückenkurs 2
K (Solution 1.3:7 moved to Lösung 1.3:7: Robot: moved page) |
|||
| Zeile 1: | Zeile 1: | ||
| - | + | Das Verfahren wird hier deutlich illustriert: | |
[[Image:1_3_7_1_1.gif|center]] | [[Image:1_3_7_1_1.gif|center]] | ||
| - | + | Nachdem wir den Volumen des Kegels maximieren wollen, definieren wir die Maße des Kegels. | |
[[Image:1_3_7_1_2.gif|center]] | [[Image:1_3_7_1_2.gif|center]] | ||
| - | + | Mit diesen Maßen wird der Volumen des Kegels, | |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
| - | V &= \frac{1}{3}\text{( | + | V &= \frac{1}{3}\text{(Fläche des Kreises)}\cdot\text{(Höhe)}\\[5pt] |
&= \frac{1}{3}\pi r^{2}h\,\textrm{.} | &= \frac{1}{3}\pi r^{2}h\,\textrm{.} | ||
\end{align}</math>}} | \end{align}</math>}} | ||
| - | + | Wir müssen jetzt den Radius <math>r</math> und die Höhe <math>h</math> durch den Winkel <math>\alpha</math> schreiben, sodass wir den Volumen <math>V</math> als Funktion von <math>\alpha </math> schreiben können. | |
| - | + | Schneiden wir einen Kreissektor mit dem Winkel <math>\alpha</math> von den Kreis weg, wird der Radius des über gebliebenen Kreises | |
| - | <math>(2\pi-\alpha)R</math>, | + | <math>(2\pi-\alpha)R</math> sein, wo <math>R</math> der ursprüngliche Radius ist. |
[[Image:1_3_7_1_3.gif|center]] | [[Image:1_3_7_1_3.gif|center]] | ||
| - | + | Der Umfang des oberen Kreises ist aber auch | |
| - | <math>2\pi r</math>, | + | <math>2\pi r</math>, und also haben wir |
{{Abgesetzte Formel||<math>2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}</math>}} | {{Abgesetzte Formel||<math>2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.}</math>}} | ||
| - | + | Jetzt haben wir also den neuen Radius <math>r</math> als Funktion von den Winkel | |
| - | <math>\alpha</math> | + | <math>\alpha</math> und den ursprünglichen Radius <math>R</math> geschrieben. |
| - | + | Um die Höhe zu beschreiben, benutzen wir das Gesetz des Pythagoras | |
[[Image:1_3_7_1_4.gif||center]] | [[Image:1_3_7_1_4.gif||center]] | ||
| - | + | Also haben wir | |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
| Zeile 41: | Zeile 41: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
| - | + | Jetzt haben wir den Radius <math>r</math> und die Höhe <math>h</math> als Funktionen von | |
| - | <math>\alpha</math> | + | <math>\alpha</math> und <math>R</math>, geschrieben. Der Volumen des Kegels ist also |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
| Zeile 50: | Zeile 50: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
| - | + | Unser Problem ist jetzt: | |
| - | :: | + | ::Maximiere <math>V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,</math>, wo <math>0\le \alpha \le 2\pi\,</math>. |
| - | + | Bevor wir anfangen die Funktion abzuleiten, sehen wir dass dar Winkel | |
| - | <math>\alpha</math> | + | <math>\alpha</math> nur in |
| - | <math>(2\pi-\alpha)/2\pi</math>, | + | <math>(2\pi-\alpha)/2\pi</math>-Termen auftritt, und also können wir den Volumen genauso in Bezug auf den Variabel <math>x=(2\pi-\alpha)/2\pi</math> maximieren, um das Problem zu vereinfachen, |
| - | :: | + | ::Maximiere <math>V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\,</math>, wenn <math>0\le x\le 1\,</math>. |
| - | + | Wenn <math>x=0</math> oder <math>x=1</math>, ist der Volumen null, und nachdem die Funktion überall außer in <math>x=1</math> ableitbar ist, nimmt der Volumen sein Maxima an einen stationären Punkt an. | |
| - | + | Wir leiten die Funktion ab, | |
{{Abgesetzte Formel||<math>V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,,</math>}} | {{Abgesetzte Formel||<math>V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,,</math>}} | ||
| - | + | und vereinfachen den Ausdruck, indem wir so viele Faktoren wir möglich herausziehen, | |
{{Abgesetzte Formel||<math>\begin{align} | {{Abgesetzte Formel||<math>\begin{align} | ||
| Zeile 74: | Zeile 74: | ||
\end{align}</math>}} | \end{align}</math>}} | ||
| - | + | Die Ableitung ist null wenn <math>x=0</math> (dies ist auch ein Endpunkt) oder wenn <math>2-3x^2=0</math>, also wenn <math>x=\sqrt{2/3}\,</math>. (Der Punkt <math>x=-\sqrt{2/3}</math> liegt außerhalb des Gebietes <math>0\le x\le 1</math>.) | |
| - | + | ||
| - | + | ||
| + | Durch einer Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren, | ||
{| border="1" cellpadding="5" cellspacing="0" align="center" | {| border="1" cellpadding="5" cellspacing="0" align="center" | ||
| Zeile 111: | Zeile 110: | ||
| - | + | und erhalten dadurch das Vorzeichen der Ableitung selbst | |
| Zeile 138: | Zeile 137: | ||
|} | |} | ||
| - | + | Wir sehen hier dass <math>x=\sqrt{2/3}</math> ein globales Maxima ist. <math>x = \sqrt{2/3}</math> entspricht den Winkel <math>\alpha</math>: | |
| - | + | ||
{{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ \text{radians.}</math>}} | {{Abgesetzte Formel||<math>\sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ \text{radians.}</math>}} | ||
Version vom 12:45, 27. Apr. 2009
Das Verfahren wird hier deutlich illustriert:
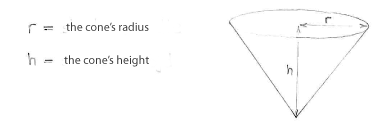
Nachdem wir den Volumen des Kegels maximieren wollen, definieren wir die Maße des Kegels.
Mit diesen Maßen wird der Volumen des Kegels,
| \displaystyle \begin{align}
V &= \frac{1}{3}\text{(Fläche des Kreises)}\cdot\text{(Höhe)}\\[5pt] &= \frac{1}{3}\pi r^{2}h\,\textrm{.} \end{align} |
Wir müssen jetzt den Radius \displaystyle r und die Höhe \displaystyle h durch den Winkel \displaystyle \alpha schreiben, sodass wir den Volumen \displaystyle V als Funktion von \displaystyle \alpha schreiben können.
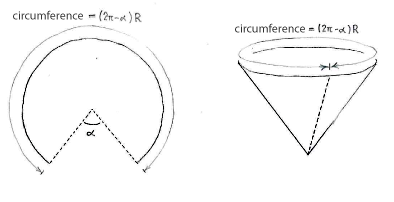
Schneiden wir einen Kreissektor mit dem Winkel \displaystyle \alpha von den Kreis weg, wird der Radius des über gebliebenen Kreises \displaystyle (2\pi-\alpha)R sein, wo \displaystyle R der ursprüngliche Radius ist.
Der Umfang des oberen Kreises ist aber auch \displaystyle 2\pi r, und also haben wir
| \displaystyle 2\pi r = (2\pi-\alpha)R\quad\Leftrightarrow\quad r = \frac{2\pi -\alpha}{2\pi}\,R\,\textrm{.} |
Jetzt haben wir also den neuen Radius \displaystyle r als Funktion von den Winkel \displaystyle \alpha und den ursprünglichen Radius \displaystyle R geschrieben.
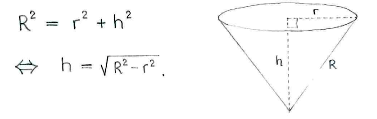
Um die Höhe zu beschreiben, benutzen wir das Gesetz des Pythagoras
Also haben wir
| \displaystyle \begin{align}
h &= \sqrt{R^2-\Bigl(\frac{2\pi-\alpha}{2\pi}\,R\Bigr)^2}\\[5pt] &= \sqrt{R^2-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2R^2}\\[5pt] &= R\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,\textrm{.} \end{align} |
Jetzt haben wir den Radius \displaystyle r und die Höhe \displaystyle h als Funktionen von \displaystyle \alpha und \displaystyle R, geschrieben. Der Volumen des Kegels ist also
| \displaystyle \begin{align}
V &= \frac{1}{3}\pi r^2 h\\[5pt] &= \frac{1}{3}\pi \Bigl(\frac{2\pi-\alpha}{2\pi}R\Bigr)^2 R\sqrt{1-\Bigl( \frac{2\pi-\alpha}{2\pi}\Bigr)^2}\\[5pt] &= \frac{1}{3}\pi R^3\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2 \sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,\textrm{.} \end{align} |
Unser Problem ist jetzt:
- Maximiere \displaystyle V(\alpha) = \frac{1}{3}\pi R^3 \Bigl(\frac{2\pi-\alpha}{2\pi} \Bigr)^2\sqrt{1-\Bigl(\frac{2\pi-\alpha}{2\pi}\Bigr)^2}\,, wo \displaystyle 0\le \alpha \le 2\pi\,.
Bevor wir anfangen die Funktion abzuleiten, sehen wir dass dar Winkel \displaystyle \alpha nur in \displaystyle (2\pi-\alpha)/2\pi-Termen auftritt, und also können wir den Volumen genauso in Bezug auf den Variabel \displaystyle x=(2\pi-\alpha)/2\pi maximieren, um das Problem zu vereinfachen,
- Maximiere \displaystyle V(x) = \frac{1}{3}\pi R^3x^2\sqrt{1-x^2}\,, wenn \displaystyle 0\le x\le 1\,.
Wenn \displaystyle x=0 oder \displaystyle x=1, ist der Volumen null, und nachdem die Funktion überall außer in \displaystyle x=1 ableitbar ist, nimmt der Volumen sein Maxima an einen stationären Punkt an.
Wir leiten die Funktion ab,
| \displaystyle V'(x) = \frac{1}{3}\pi R^3\cdot 2x\cdot \sqrt{1-x^2} + \frac{1}{3}\pi R^3x^2\cdot\frac{1}{2\sqrt{1-x^2}}\cdot (-2x)\,, |
und vereinfachen den Ausdruck, indem wir so viele Faktoren wir möglich herausziehen,
| \displaystyle \begin{align}
V'(x) &= \frac{2}{3}\pi R^3x\sqrt{1-x^2} - \frac{1}{3}\pi R^3x^3\frac{1}{\sqrt{1-x^2}}\\[5pt] &= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}\bigl[ 2(1-x^2)-x^2\bigr]\\[5pt] &= \frac{1}{3}\pi R^3\frac{x}{\sqrt{1-x^2}}(2-3x^2)\,\textrm{.} \end{align} |
Die Ableitung ist null wenn \displaystyle x=0 (dies ist auch ein Endpunkt) oder wenn \displaystyle 2-3x^2=0, also wenn \displaystyle x=\sqrt{2/3}\,. (Der Punkt \displaystyle x=-\sqrt{2/3} liegt außerhalb des Gebietes \displaystyle 0\le x\le 1.)
Durch einer Vorzeichentabelle erhalten wir die Vorzeichen der Faktoren,
| \displaystyle x | \displaystyle 0 | \displaystyle \sqrt{\tfrac{2}{3}} | \displaystyle 1 | ||
| \displaystyle x | \displaystyle 0 | \displaystyle + | \displaystyle + | \displaystyle + | \displaystyle + |
| \displaystyle \sqrt{1-x^2} | \displaystyle + | \displaystyle + | \displaystyle + | \displaystyle + | \displaystyle 0 |
| \displaystyle 2-3x^2 | \displaystyle + | \displaystyle + | \displaystyle 0 | \displaystyle - | \displaystyle - |
und erhalten dadurch das Vorzeichen der Ableitung selbst
| \displaystyle x | \displaystyle 0 | \displaystyle \sqrt{\tfrac{2}{3}} | \displaystyle 1 | ||
| \displaystyle V'(x) | \displaystyle 0 | \displaystyle + | \displaystyle 0 | \displaystyle - | |
| \displaystyle V(x) | \displaystyle 0 | \displaystyle \nearrow | \displaystyle \tfrac{4}{9\sqrt{3}}\pi R^3 | \displaystyle \searrow | \displaystyle 0 |
Wir sehen hier dass \displaystyle x=\sqrt{2/3} ein globales Maxima ist. \displaystyle x = \sqrt{2/3} entspricht den Winkel \displaystyle \alpha:
| \displaystyle \sqrt{\frac{2}{3}}=\frac{2\pi-\alpha }{2\pi}\quad \Leftrightarrow\quad \alpha = 2\pi \bigl(1-\sqrt{2/3}\,\bigr)\ \text{radians.} |