Lösung 1.3:1c

Aus Online Mathematik Brückenkurs 2

(Unterschied zwischen Versionen)
Wechseln zu: Navigation, Suche
K (Solution 1.3:1c moved to Lösung 1.3:1c: Robot: moved page)
Zeile 1: Zeile 1:
-
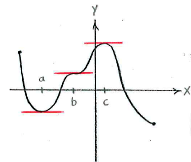
The function has zero derivative at three points, <math>x=a</math>, <math>x=b</math> and <math>x=c</math> (see picture below), which are therefore the critical points of the function.
+
Die Ableitung der Funktion hat drei Nullstellen, <math>x=a</math>, <math>x=b</math> und <math>x=c</math> (siehe Figur). Dies sind die stationären Punkte.
[[Image:1_3_1_c1.gif|center]]
[[Image:1_3_1_c1.gif|center]]
-
The point <math>x=b</math> is an inflexion point because the derivative is positive in a neighbourhood both to the left and right.
+
Der Punkt <math>x=b</math> ist ein Sattelpunkt nachdem die Ableitung links und rechts vom Punkt positiv ist.
-
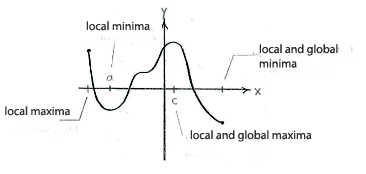
At the left endpoint of the interval of definition and at <math>x=c</math>, the function has local maximum points , because the function takes lower values at all points in the vicinity of these points. At the point <math>x=a</math> and the right endpoint, the function has local minimum points.
+
Am linken Endpunkt, und im Punkt <math>x=c</math> hat die Funktion lokale Minima. Am rechten Endpunkt und im Punkt <math>x=a</math> hat die Funktion lokale Maxima.
-
Also, we see that <math>x=c</math> is a global maximum (the function takes its largest value there) and the right endpoint is a global minimum.
+
Von diesen Punkten ist <math>x=c</math> das globale Maxima, und der rechte Endpunkt das globale Minima.
[[Image:1_3_1_c2.gif|center]]
[[Image:1_3_1_c2.gif|center]]
-
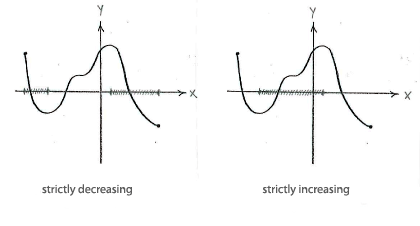
Between the left endpoint and <math>x=a</math>, as well as between <math>x=c</math>
+
Zwischen den linken Endpunkt und <math>x=a</math>, sowohl wie zwischen <math>x=c</math> und den rechten Endpunkt. ist die Funktion streng fallend, während die Funktion streng steigend zwischen <math>x=a</math> und <math>x=c</math> ist.
-
and the right endpoint, the function is strictly decreasing (the larger <math>x</math> is, the smaller <math>f(x)</math> becomes), whilst the function is strictly increasing between <math>x=a</math> and <math>x=c</math> (the graph flattens out at <math>x=b</math>, but it isn't constant there).
+
[[Image:1_3_1_c3.gif|center]]
[[Image:1_3_1_c3.gif|center]]

Version vom 15:05, 26. Apr. 2009

Die Ableitung der Funktion hat drei Nullstellen, \displaystyle x=a, \displaystyle x=b und \displaystyle x=c (siehe Figur). Dies sind die stationären Punkte.

Der Punkt \displaystyle x=b ist ein Sattelpunkt nachdem die Ableitung links und rechts vom Punkt positiv ist.

Am linken Endpunkt, und im Punkt \displaystyle x=c hat die Funktion lokale Minima. Am rechten Endpunkt und im Punkt \displaystyle x=a hat die Funktion lokale Maxima.

Von diesen Punkten ist \displaystyle x=c das globale Maxima, und der rechte Endpunkt das globale Minima.

Zwischen den linken Endpunkt und \displaystyle x=a, sowohl wie zwischen \displaystyle x=c und den rechten Endpunkt. ist die Funktion streng fallend, während die Funktion streng steigend zwischen \displaystyle x=a und \displaystyle x=c ist.

Von „http://wiki.sommarmatte.se/wikis/2009/bridgecourse2-TU-Berlin/index.php/L%C3%B6sung_1.3:1c“