Lösung 3.2:2e
Aus Online Mathematik Brückenkurs 2
(Unterschied zwischen Versionen)
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
K (Solution 3.2:2e moved to Lösung 3.2:2e: Robot: moved page) |
Version vom 10:36, 11. Mär. 2009
Because the expression contains both \displaystyle z and \displaystyle \bar{z}, we write out \displaystyle z=x+iy, where \displaystyle x is the real part of \displaystyle z and \displaystyle y is the imaginary part. Thus, we have
- \displaystyle \mathop{\rm Re}z = x
- \displaystyle i+\bar{z} = i+(x-iy) = x+(1-y)i
and the condition becomes
| \displaystyle x=x+(1-y)i\quad\Leftrightarrow\quad 0=(1-y)i |
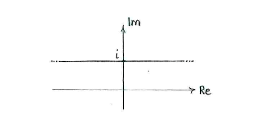
which means that \displaystyle y=1.
The set therefore consists of all complex numbers with imaginary part 1.