Lösung 3.3:2c
Aus Online Mathematik Brückenkurs 2
K |
K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) |
||
| Zeile 1: | Zeile 1: | ||
We write <math>z</math> and the right-hand side <math>-1-i</math> in polar form | We write <math>z</math> and the right-hand side <math>-1-i</math> in polar form | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\begin{align} |
z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] | z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] | ||
-1-i &= \sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4}\Bigr)\,\textrm{.} | -1-i &= \sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4}\Bigr)\,\textrm{.} | ||
| Zeile 8: | Zeile 8: | ||
Using de Moivre's formula, the equation can now be written as | Using de Moivre's formula, the equation can now be written as | ||
| - | {{ | + | {{Abgesetzte Formel||<math>r^5(\cos 5\alpha + i\sin 5\alpha) = \sqrt{2}\Bigl(\cos \frac{5\pi}{4} + i\sin\frac{5\pi}{4}\Bigr)\,\textrm{.}</math>}} |
If we identify the magnitude and argument on both sides, we get | If we identify the magnitude and argument on both sides, we get | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\left\{\begin{align} |
r^5 &= \sqrt{2}\,,\\[5pt] | r^5 &= \sqrt{2}\,,\\[5pt] | ||
5\alpha &= \frac{5\pi}{4} + 2n\pi\,,\quad\text{(n is an arbitrary integer).} | 5\alpha &= \frac{5\pi}{4} + 2n\pi\,,\quad\text{(n is an arbitrary integer).} | ||
| Zeile 21: | Zeile 21: | ||
This gives that | This gives that | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\left\{\begin{align} |
r &= \sqrt[5]{2} = \bigl(2^{1/2}\bigr)^{1/5} = 2^{1/10}\,,\\[5pt] | r &= \sqrt[5]{2} = \bigl(2^{1/2}\bigr)^{1/5} = 2^{1/10}\,,\\[5pt] | ||
\alpha &= \frac{1}{5}\Bigl(\frac{5\pi}{4}+2n\pi\Bigr) = \frac{\pi}{4} + \frac{2n\pi}{5}\,,\quad\text{(n is an arbitrary integer).} | \alpha &= \frac{1}{5}\Bigl(\frac{5\pi}{4}+2n\pi\Bigr) = \frac{\pi}{4} + \frac{2n\pi}{5}\,,\quad\text{(n is an arbitrary integer).} | ||
| Zeile 28: | Zeile 28: | ||
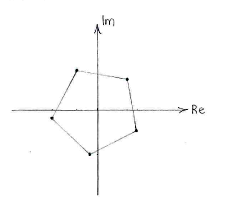
If we investigate the argument <math>\alpha</math> more closely, we see that it assumes essentially only five different values, | If we investigate the argument <math>\alpha</math> more closely, we see that it assumes essentially only five different values, | ||
| - | {{ | + | {{Abgesetzte Formel||<math>\frac{\pi}{4}</math>, <math>\quad\frac{\pi}{4}+\frac{2\pi}{5}</math>, <math>\quad\frac{\pi}{4}+\frac{4\pi}{5}</math>, <math>\quad\frac{\pi}{4}+\frac{6\pi}{5}\quad</math> and <math>\quad\frac{\pi}{4}+\frac{8\pi}{5}</math>}} |
since these angle values then repeat to within a multiple of <math>2\pi</math>. | since these angle values then repeat to within a multiple of <math>2\pi</math>. | ||
| Zeile 34: | Zeile 34: | ||
In summary, the solutions are | In summary, the solutions are | ||
| - | {{ | + | {{Abgesetzte Formel||<math>z = 2^{1/10}\,\Bigl(\cos\Bigl(\frac{\pi}{4}+\frac{2n\pi}{5}\Bigr) + i\sin\Bigl(\frac{\pi}{4}+\frac{2n\pi}{5}\Bigr)\Bigr)\,,</math>}} |
for <math>n=0</math>, <math>1</math>, <math>2</math>, <math>3</math> and | for <math>n=0</math>, <math>1</math>, <math>2</math>, <math>3</math> and | ||
Version vom 13:11, 10. Mär. 2009
We write \displaystyle z and the right-hand side \displaystyle -1-i in polar form
| \displaystyle \begin{align}
z &= r(\cos\alpha + i\sin\alpha)\,,\\[5pt] -1-i &= \sqrt{2}\Bigl(\cos\frac{5\pi}{4} + i\sin\frac{5\pi}{4}\Bigr)\,\textrm{.} \end{align} |
Using de Moivre's formula, the equation can now be written as
| \displaystyle r^5(\cos 5\alpha + i\sin 5\alpha) = \sqrt{2}\Bigl(\cos \frac{5\pi}{4} + i\sin\frac{5\pi}{4}\Bigr)\,\textrm{.} |
If we identify the magnitude and argument on both sides, we get
| \displaystyle \left\{\begin{align}
r^5 &= \sqrt{2}\,,\\[5pt] 5\alpha &= \frac{5\pi}{4} + 2n\pi\,,\quad\text{(n is an arbitrary integer).} \end{align}\right. |
(The arguments \displaystyle 5\alpha and \displaystyle 5\pi/4 can differ by a multiple of \displaystyle 2\pi and still correspond to the same complex number.)
This gives that
| \displaystyle \left\{\begin{align}
r &= \sqrt[5]{2} = \bigl(2^{1/2}\bigr)^{1/5} = 2^{1/10}\,,\\[5pt] \alpha &= \frac{1}{5}\Bigl(\frac{5\pi}{4}+2n\pi\Bigr) = \frac{\pi}{4} + \frac{2n\pi}{5}\,,\quad\text{(n is an arbitrary integer).} \end{align}\right. |
If we investigate the argument \displaystyle \alpha more closely, we see that it assumes essentially only five different values,
| \displaystyle \frac{\pi}{4}, \displaystyle \quad\frac{\pi}{4}+\frac{2\pi}{5}, \displaystyle \quad\frac{\pi}{4}+\frac{4\pi}{5}, \displaystyle \quad\frac{\pi}{4}+\frac{6\pi}{5}\quad and \displaystyle \quad\frac{\pi}{4}+\frac{8\pi}{5} |
since these angle values then repeat to within a multiple of \displaystyle 2\pi.
In summary, the solutions are
| \displaystyle z = 2^{1/10}\,\Bigl(\cos\Bigl(\frac{\pi}{4}+\frac{2n\pi}{5}\Bigr) + i\sin\Bigl(\frac{\pi}{4}+\frac{2n\pi}{5}\Bigr)\Bigr)\,, |
for \displaystyle n=0, \displaystyle 1, \displaystyle 2, \displaystyle 3 and \displaystyle 4.