Aus Online Mathematik Brückenkurs 2

Version vom 09:51, 29. Okt. 2008 (bearbeiten) Tek (Diskussion | Beiträge) K ← Zum vorherigen Versionsunterschied		Version vom 13:08, 10. Mär. 2009 (bearbeiten) (rückgängig) Tekbot (Diskussion | Beiträge) K (Robot: Automated text replacement (-{{Displayed math +{{Abgesetzte Formel)) Zum nächsten Versionsunterschied →
Zeile 10:		Zeile 10:
	<math>1+i</math> to <math>\text{3}i</math> is		<math>1+i</math> to <math>\text{3}i</math> is
-	{{Displayed math||<math>3i-(1+i) = -1+2i</math>}}	+	{{Abgesetzte Formel||<math>3i-(1+i) = -1+2i</math>}}
	and we obtain the fourth corner if we add this vector to the corner <math>3+2i</math>,		and we obtain the fourth corner if we add this vector to the corner <math>3+2i</math>,
-	{{Displayed math||<math>3+2i+(-1+2i) = 2+4i\,\textrm{.}</math>}}	+	{{Abgesetzte Formel||<math>3+2i+(-1+2i) = 2+4i\,\textrm{.}</math>}}

---

Version vom 13:08, 10. Mär. 2009

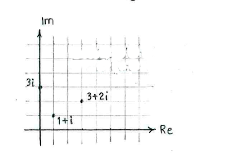
If we mark the three complex numbers in the plane, we see that the fourth corner will have \displaystyle 3+2i and \displaystyle 3i as neighbouring corners.

In order to find the fourth corner, we use the fact that in a square opposite sides are parallel and all sides have the same length. This means that the vector from \displaystyle 1+i to \displaystyle 3i is equal to the vector from \displaystyle 3+2i to the fourth corner.

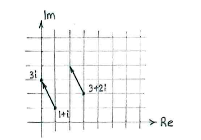
If we interpret the complex numbers as vectors, this means that the vector from \displaystyle 1+i to \displaystyle \text{3}i is

\displaystyle 3i-(1+i) = -1+2i

and we obtain the fourth corner if we add this vector to the corner \displaystyle 3+2i,

\displaystyle 3+2i+(-1+2i) = 2+4i\,\textrm{.}